Example: beam01

We build the model based a few parameters as follows.

        # initialize a system model
        SpanLength = 10.0 * 12
        w =  -1.0   # distributed load (positive if acting in local y-direction
        P =   -40.0   # center point load (uses global system)

        Nelems = 4    # number of elements
        params = {'E': 29000., 'A': 4.7, 'I':103}

All mesh creation is based solely on the above parameters to allow for easy manipulation of the model.

The actual model is built by the block below.

        model = System()

        # meshing parameters
        Le = SpanLength / Nelems
        Xnode = 0.0
        Ynode = 0.0

        # create left node
        nd0 = Node(Xnode, Ynode)
        model += nd0

        ndP = None

        # initialization for node and element creation
        ndi = nd0

        for e in range(Nelems):
            # create next node
            Xnode += Le
            ndj = Node(Xnode, Ynode)
            model += ndj

            # remember center node for loading
            if Xnode <= SpanLength/2:
                ndP = ndj

            # create elements
            elem = Beam2D(ndi, ndj, ElasticSection(params))
            model += elem

            # load the element
            elem.setDistLoad(w)

            # shift one node to the right
            ndi = ndj

Line 8 instantiates one model space.

Lines 16, 25-27 create the nodes, and lines 17 and 28 add them to the model space.

Lines 34-36 create the elements and add them to the model space. You only need to create variables for Node and Element objects, respectively, if you need to either add or retrieve information from that object later.

The support conditions are defined by providing the respective information directly to the supported nodes. The following lines add a pin support on the first node and a roller on the last one.

        # define support(s)
        nd0.fixDOF('ux', 'uy')     # pin support left end
        ndj.fixDOF('uy')           # roller support right end

We still need to apply the point load at the center node. In the above element creation loop, we identified the node closest to the center node (will be exactly at the center if Nelem is an even number) and stored it as ndP. Apply the nodal force at ndP by the next lines to complete the model.

        # add point loads
        # .. load only the center node
        if ndP:
            ndP.setLoad([0.0, P], ('ux', 'uy'))

The system equations are solved by a single call to the solver:

        # analyze the model
        model.solve()

You can obtain a debug-style report on the state of the system:

        # write out report
        model.report()

Resulting in an output like (may change as the code evolves).

System Analysis Report
=======================

Nodes:
---------------------
  Node 0: {'uy': 0, 'rz': 1}
          x:[0. 0.], fix:['ux', 'uy'],
          P:[0. 0.], u:[ 0.         -0.03615668]
  Node 1: {'uy': 0, 'rz': 1}
          x:[30.  0.], fix:[],
          P:[0. 0.], u:[-0.97547707 -0.02561098]
  Node 2: {'uy': 0, 'rz': 1}
          x:[60.  0.], fix:[],
          P:[-40.   0.], u:[-1.38600603e+00 -1.37017950e-17]
  Node 3: {'uy': 0, 'rz': 1}
          x:[90.  0.], fix:[],
          P:[0. 0.], u:[-0.97547707  0.02561098]
  Node 4: {'uy': 0, 'rz': 1}
          x:[120.   0.], fix:['uy'],
          P:[0. 0.], u:[0.         0.03615668]

Elements:
---------------------
  Beam2D: node 0 to node 1:
     material ElasticSection properties: {'E': 29000.0, 'A': 4.7, 'I': 103, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:65.0 Mi:-74.99999999999909 Vj:-65.0 Mj:2024.999999999989
  Beam2D: node 1 to node 2:
     material ElasticSection properties: {'E': 29000.0, 'A': 4.7, 'I': 103, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:34.999999999999886 Mi:-2024.9999999999864 Vj:-34.999999999999886 Mj:3074.999999999981
  Beam2D: node 2 to node 3:
     material ElasticSection properties: {'E': 29000.0, 'A': 4.7, 'I': 103, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:-34.999999999999716 Mi:-3074.99999999998 Vj:34.999999999999716 Mj:2024.9999999999936
  Beam2D: node 3 to node 4:
     material ElasticSection properties: {'E': 29000.0, 'A': 4.7, 'I': 103, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:-65.00000000000023 Mi:-2024.9999999999936 Vj:65.00000000000023 Mj:74.99999999999818

An easier way to look at the simulation results are plots. A deformed system plot is obtained using the model.plot() directive. If a filename is given, the plot will be saved to the harddrive using that file name. An internal force plot is created equally simple.

        # create plots
        model.plot(factor=10., filename="beam01_deformed.png")

        model.beamValuePlot('V', filename="beam01_shear.png")
        model.beamValuePlot('M', filename="beam01_moment.png")

Showing file beam01_deformed.png

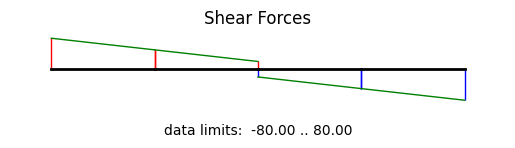
Showing file beam01_shear.png

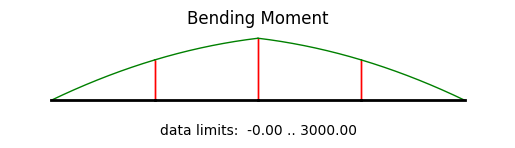
Showing file beam01_moment.png

Importing the example

from femedu.examples.beams.beam01 import *

# load the example
ex = ExampleBeam01()

More beam examples: Beam Examples