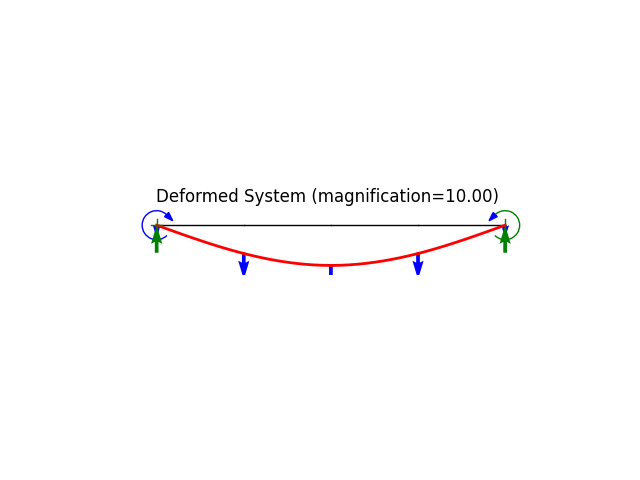
Single span beam under uniform load.

The system is statically determined and allows for easy validation of calculated deformation, reactions and internal forces.

Author: Peter Mackenzie-Helnwein

from femedu.examples.Example import *

from femedu.domain.System import *
from femedu.domain.Node import *
from femedu.elements.linear import Beam2D
from femedu.materials.ElasticSection import *


class ExampleBeam01(Example):

    def problem(self):
        # initialize a system model
        SpanLength = 10.0 * 12
        w =  -1.0   # distributed load (positive if acting in local y-direction
        P =   -40.0   # center point load (uses global system)

        Nelems = 4    # number of elements
        params = {'E': 29000., 'A': 4.7, 'I':103}

        model = System()

        # meshing parameters
        Le = SpanLength / Nelems
        Xnode = 0.0
        Ynode = 0.0

        # create left node
        nd0 = Node(Xnode, Ynode)
        model += nd0

        ndP = None

        # initialization for node and element creation
        ndi = nd0

        for e in range(Nelems):
            # create next node
            Xnode += Le
            ndj = Node(Xnode, Ynode)
            model += ndj

            # remember center node for loading
            if Xnode <= SpanLength/2:
                ndP = ndj

            # create elements
            elem = Beam2D(ndi, ndj, ElasticSection(params))
            model += elem

            # load the element
            elem.setDistLoad(w)

            # shift one node to the right
            ndi = ndj

        # define support(s)
        nd0.fixDOF('ux', 'uy')     # pin support left end
        ndj.fixDOF('uy')           # roller support right end

        # add point loads
        # .. load only the center node
        if ndP:
            ndP.setLoad([0.0, P], ('ux', 'uy'))

        # analyze the model
        model.solve()

        # write out report
        model.report()

        # create plots
        model.plot(factor=10., filename="beam01_deformed.png", show_bc=1, show_reactions=1)

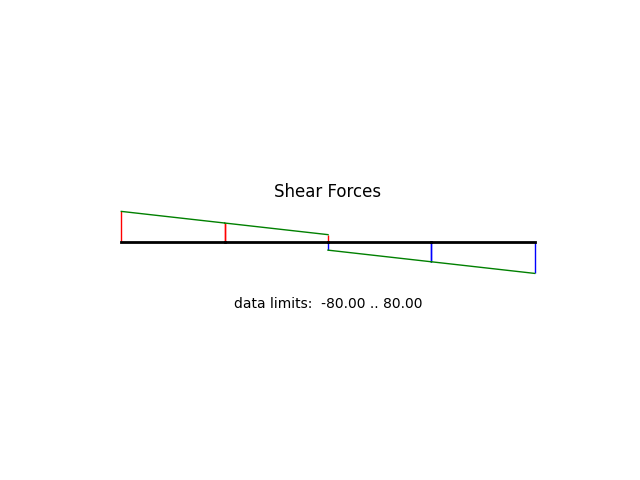
        model.beamValuePlot('V', filename="beam01_shear.png")
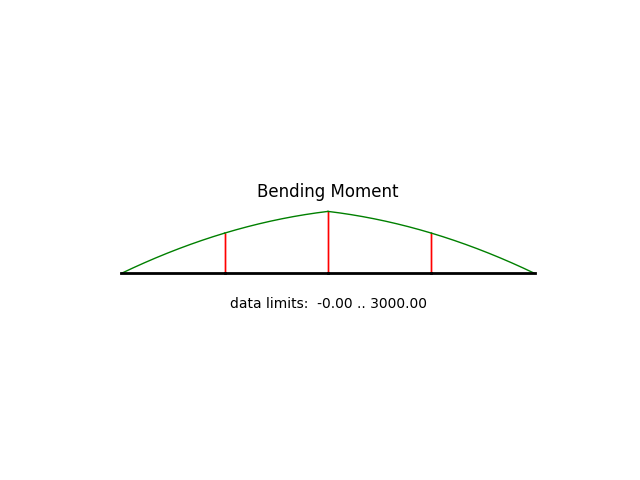
        model.beamValuePlot('M', filename="beam01_moment.png")

Run the example by creating an instance of the problem and executing it by calling Example.run()

if __name__ == "__main__":
    ex = ExampleBeam01()
    ex.run()

• 
• 
• 

System Analysis Report
=======================

Nodes:
---------------------
  Node_12:
      x:    [0.000 0.000]
      fix:  ['ux', 'uy']
      u:    [0.000 -0.036]
  Node_13:
      x:    [30.000 0.000]
      u:    [-0.975 -0.026]
  Node_14:
      x:    [60.000 0.000]
      P:    [-40.000 0.000]
      u:    [-1.386 0.000]
  Node_15:
      x:    [90.000 0.000]
      u:    [-0.975 0.026]
  Node_16:
      x:    [120.000 0.000]
      fix:  ['uy']
      u:    [0.000 0.036]

Elements:
---------------------
  Beam2D: Node_12 to Node_13:
     material ElasticSection properties: {'E': 29000.0, 'A': 4.7, 'I': 103, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:65.0 Mi:-74.99999999999818 Vj:-65.0 Mj:2024.9999999999927
  Beam2D: Node_13 to Node_14:
     material ElasticSection properties: {'E': 29000.0, 'A': 4.7, 'I': 103, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:35.0 Mi:-2024.9999999999952 Vj:-35.0 Mj:3074.9999999999877
  Beam2D: Node_14 to Node_15:
     material ElasticSection properties: {'E': 29000.0, 'A': 4.7, 'I': 103, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:-35.0 Mi:-3074.999999999988 Vj:35.0 Mj:2024.999999999991
  Beam2D: Node_15 to Node_16:
     material ElasticSection properties: {'E': 29000.0, 'A': 4.7, 'I': 103, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:-64.99999999999977 Mi:-2024.9999999999882 Vj:64.99999999999977 Mj:75.00000000000546