Three-span continuous beam under uniform load.

The system is statically indeterminate but simple enough to validate deformation, reactions and internal forces.

Author: Peter Mackenzie-Helnwein

from femedu.examples.Example import *

from femedu.domain.System import *
from femedu.domain.Node import *
from femedu.elements.linear import Beam2D
from femedu.materials.ElasticSection import *

class ExampleBeam02(Example):

    def problem(self):
        # initialize a system model
        SpanLengths = [ 8.0 * 12, 10.0 * 12, 8.0 * 12 ]
        Nelems = 2     # number of elements
        params = {'E': 29000., 'A': 5, 'I':50}

        # define load
        w = -1.00

        model = System()

        # meshing parameters
        Xnode  = 0.0
        Ynode  = 0.0
        Offset = 0.0

        # create left node
        nd0 = Node(Xnode, Ynode)
        nd0.fixDOF('ux', 'uy')     # pin support left end
        model += nd0

        # initialization for node and element creation
        ndi = nd0

        for SpanLength in SpanLengths:

            Le = SpanLength / Nelems

            for e in range(Nelems):
                # create next node
                Xnode += Le
                ndj = Node(Xnode, Ynode)
                model += ndj

                # create elements
                elem = Beam2D(ndi, ndj, ElasticSection(params))
                model += elem

                # load the element with a uniform load
                elem.setDistLoad(w)

                # shift one node to the right
                ndi = ndj

            # define support(s)
            ndj.fixDOF('uy')           # roller support right end

            # move on to the next span
            Offset = Xnode

        # done building the model

        # analyze the model
        model.solve()

        # write out report
        model.report()

        # create plots
        model.plot(factor=100., filename="beam02_deformed.png", show_bc=1, show_reactions=1)

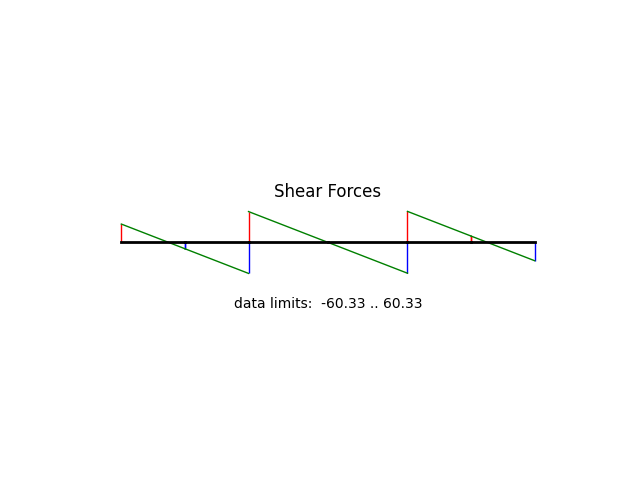
        model.beamValuePlot('V', filename="beam02_shear.png")
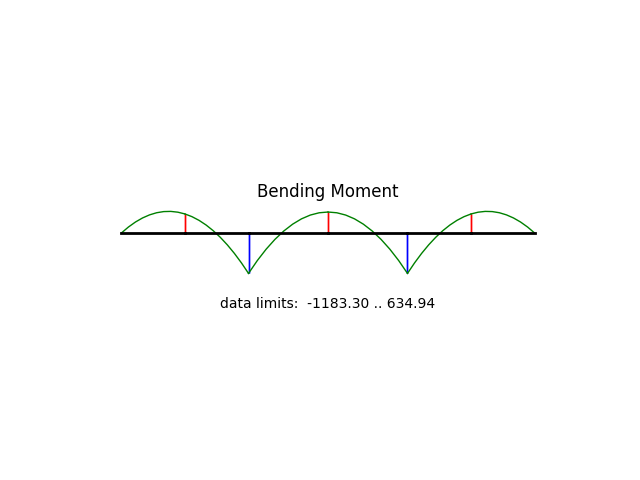
        model.beamValuePlot('M', filename="beam02_moment.png")

Run the example by creating an instance of the problem and executing it by calling Example.run()

if __name__ == "__main__":
    ex = ExampleBeam02()
    ex.run()

• 
• 
• 

System Analysis Report
=======================

Nodes:
---------------------
  Node_17:
      x:    [0. 0.]
      fix:  ['ux', 'uy']
      u:    [ 0.        -0.0123663]
  Node_18:
      x:    [48.  0.]
      u:    [-0.292646    0.00326429]
  Node_19:
      x:    [96.  0.]
      fix:  ['uy']
      u:    [ 0.         -0.00069085]
  Node_20:
      x:    [156.   0.]
      u:    [-3.93139430e-01 -4.24063967e-19]
  Node_21:
      x:    [216.   0.]
      fix:  ['uy']
      u:    [0.         0.00069085]
  Node_22:
      x:    [264.   0.]
      u:    [-0.292646   -0.00326429]
  Node_23:
      x:    [312.   0.]
      fix:  ['uy']
      u:    [0.        0.0123663]

Elements:
---------------------
  Beam2D: Node_17 to Node_18:
     material ElasticSection properties: {'E': 29000.0, 'A': 5, 'I': 50, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:11.673913043478258 Mi:-191.99999999999994 Vj:-11.673913043478258 Mj:752.3478260869563
  Beam2D: Node_18 to Node_19:
     material ElasticSection properties: {'E': 29000.0, 'A': 5, 'I': 50, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:-36.32608695652172 Mi:-752.347826086956 Vj:36.32608695652172 Mj:-991.3043478260865
  Beam2D: Node_19 to Node_20:
     material ElasticSection properties: {'E': 29000.0, 'A': 5, 'I': 50, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:29.999999999999993 Mi:883.3043478260867 Vj:-29.999999999999993 Mj:916.6956521739128
  Beam2D: Node_20 to Node_21:
     material ElasticSection properties: {'E': 29000.0, 'A': 5, 'I': 50, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:-29.99999999999999 Mi:-916.6956521739127 Vj:29.99999999999999 Mj:-883.3043478260865
  Beam2D: Node_21 to Node_22:
     material ElasticSection properties: {'E': 29000.0, 'A': 5, 'I': 50, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:36.32608695652173 Mi:991.3043478260865 Vj:-36.32608695652173 Mj:752.347826086956
  Beam2D: Node_22 to Node_23:
     material ElasticSection properties: {'E': 29000.0, 'A': 5, 'I': 50, 'nu': 0.0, 'fy': 1e+30}  strain:{'axial': 0.0, 'flexure': 0.0}   stress:{'axial': 0.0, 'flexure': 0.0}
     nodal forces: Vi:-11.673913043478258 Mi:-752.347826086956 Vj:11.673913043478258 Mj:192.0