Note
Go to the end to download the full example code.
Heat transfer through a wall
This problem demonstrates a combination of prescribed temperature on the left and prescribed flux on the right side.
Using
mesher.PatchMesher(see PatchMesher class)diffusion.Triangle(see Triangle class for Diffusion)materials.Thermal(see Diffusion Material classes)
Theory
We shall consider a stationary heat transfer problem within a wall. The inner surface of the wall, \(x=0~m\), is heated to \(200~K\), the outer surface of the wall, \(x=10~m\), to \(300~K\).
The thermal equation for the uni-directional problem can be expressed as
\[\Delta T = \frac{\partial^2 T}{\partial r^2} = 0\]
where \(\Delta\) is the Laplace operator.
The analytic solution follows as
\[T(x) = T_i + q_n \: x\]
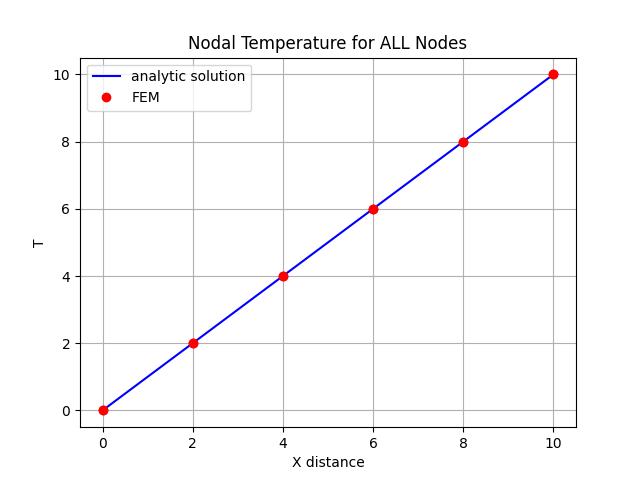
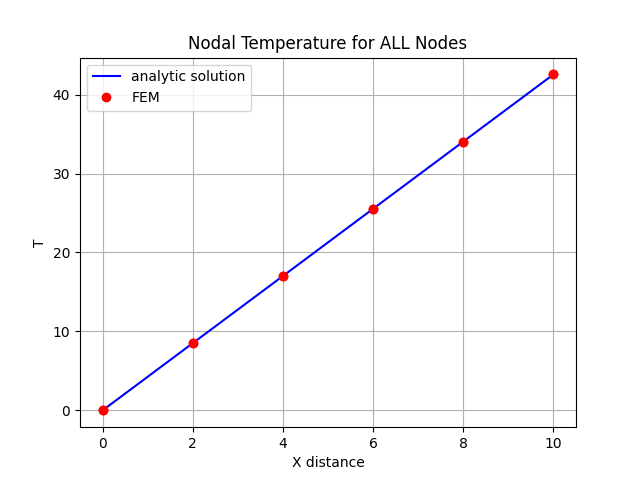
This solution will be compared against the finite element solution in the last figure.
import matplotlib.pyplot as plt
import math
import sys
import numpy as np
from femedu.examples.Example import *
from femedu.domain import *
from femedu.mesher import PatchMesher
from femedu.elements.diffusion import Triangle
from femedu.materials import Thermal
class ExampleThermal01(Example):
def problem(self):
# ========== setting mesh parameters ==============
Nx = 5 # number of elements through the wall
Ny = 1 # number of elements parallel to the wall
Lx = 10.00 # wall thickness in m
Ly = 1.00 # wall thickness in m
# ========== setting material parameters ==============
params = dict(
E = 20000., # Young's modulus
nu = 0.250, # Poisson's ratio
t = 1.00 # thickness of the plate
)
# ========== setting load parameters ==============
qn = 1.00 # uniform flux normal to x=const
# ========== setting analysis parameters ==============
target_load_level = 1.00 # reference load
max_steps = 2 # number of load steps: 2 -> [0.0, 1.0]
# define a list of target load levels
load_levels = np.linspace(0, target_load_level, max_steps)
#
# ==== Build the system model ====
#
model = System()
# create nodes
# 2 -------- 3
# | |
# | |
# | | |
# 0 -------- 1
pts = (
( 0, 0), # 0
(Lx, 0), # 1
( 0, Ly), # 2
(Lx, Ly), # 3
)
mesher = PatchMesher(model, pts[0], pts[1], pts[3], pts[2])
nodes, elements = mesher.triangleMesh(Nx, Ny, Triangle, Thermal(params))
model.plot(factor=0.0,
title='Uni-directional diffusion',
show_reactions=0, show_bc=0, show_loads=0)
model.report()
# boundary condition(s)
## find nodes at x==0
left_boundary_nodes = model.findNodesAlongLine((0.0,0.0), (0.0,1.0))
for node, dist in left_boundary_nodes:
node.fixDOF('T') # prescribed temperature at x=0.0
## complete the reference load at x=Lx (right edge)
right_boundary_faces = model.findFacesAlongLine((Lx, 0.0), (0.0, 1.0), orientation=+1)
for _, face in right_boundary_faces:
face.setFlux(qn)
# perform the analysis
model.setLoadFactor(1.0)
model.solve()
model.report()
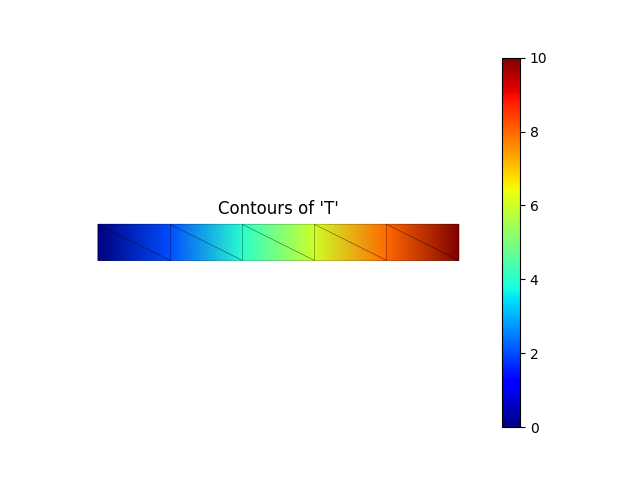
model.valuePlot('T', show_mesh=True)
# creating a path plot
R_list = []
T_list = []
for node in nodes:
X = node.getPos()
T = node.getDisp('T')
R_list.append(X[0])
T_list.append(T)
# the analytic solution for comparison
x = np.linspace(0, Lx, 21)
T = 0.0 * (1 - x/Lx) + qn * x
fig, axs = plt.subplots()
axs.plot(x,T,'-b',label="analytic solution")
axs.plot(R_list,T_list,'ro',label="FEM")
axs.set_title('Nodal Temperature for ALL Nodes')
axs.set_xlabel("X distance")
axs.set_ylabel('T')
axs.legend()
axs.grid(True)
plt.show()
Run the example by creating an instance of the problem and executing it by calling Example.run()
if __name__ == "__main__":
ex = ExampleThermal01()
ex.run()
System Analysis Report
=======================
Nodes:
---------------------
Node_224:
x: [0.000 0.000]
u: [0.000]
Node_225:
x: [2.000 0.000]
u: [0.000]
Node_226:
x: [4.000 0.000]
u: [0.000]
Node_227:
x: [6.000 0.000]
u: [0.000]
Node_228:
x: [8.000 0.000]
u: [0.000]
Node_229:
x: [10.000 0.000]
u: [0.000]
Node_230:
x: [0.000 1.000]
u: [0.000]
Node_231:
x: [2.000 1.000]
u: [0.000]
Node_232:
x: [4.000 1.000]
u: [0.000]
Node_233:
x: [6.000 1.000]
u: [0.000]
Node_234:
x: [8.000 1.000]
u: [0.000]
Node_235:
x: [10.000 1.000]
u: [0.000]
Elements:
---------------------
Triangle_341: nodes ( Node_224 Node_225 Node_230 )
material: Thermal
grad phi: x=0.000e+00 y=0.000e+00
flux: x=0.000e+00 y=0.000e+00
Triangle_342: nodes ( Node_231 Node_230 Node_225 )
material: Thermal
grad phi: x=0.000e+00 y=0.000e+00
flux: x=0.000e+00 y=0.000e+00
Triangle_343: nodes ( Node_225 Node_226 Node_231 )
material: Thermal
grad phi: x=0.000e+00 y=0.000e+00
flux: x=0.000e+00 y=0.000e+00
Triangle_344: nodes ( Node_232 Node_231 Node_226 )
material: Thermal
grad phi: x=0.000e+00 y=0.000e+00
flux: x=0.000e+00 y=0.000e+00
Triangle_345: nodes ( Node_226 Node_227 Node_232 )
material: Thermal
grad phi: x=0.000e+00 y=0.000e+00
flux: x=0.000e+00 y=0.000e+00
Triangle_346: nodes ( Node_233 Node_232 Node_227 )
material: Thermal
grad phi: x=0.000e+00 y=0.000e+00
flux: x=0.000e+00 y=0.000e+00
Triangle_347: nodes ( Node_227 Node_228 Node_233 )
material: Thermal
grad phi: x=0.000e+00 y=0.000e+00
flux: x=0.000e+00 y=0.000e+00
Triangle_348: nodes ( Node_234 Node_233 Node_228 )
material: Thermal
grad phi: x=0.000e+00 y=0.000e+00
flux: x=0.000e+00 y=0.000e+00
Triangle_349: nodes ( Node_228 Node_229 Node_234 )
material: Thermal
grad phi: x=0.000e+00 y=0.000e+00
flux: x=0.000e+00 y=0.000e+00
Triangle_350: nodes ( Node_235 Node_234 Node_229 )
material: Thermal
grad phi: x=0.000e+00 y=0.000e+00
flux: x=0.000e+00 y=0.000e+00
+ Triangle_349: nodes ( Node_228 Node_229 Node_234 )
material: Thermal
grad phi: x=0.000e+00 y=0.000e+00
flux: x=0.000e+00 y=0.000e+00
+ Triangle_350: nodes ( Node_235 Node_234 Node_229 )
material: Thermal
grad phi: x=0.000e+00 y=0.000e+00
flux: x=0.000e+00 y=0.000e+00
+ Triangle_350: nodes ( Node_235 Node_234 Node_229 )
material: Thermal
grad phi: x=0.000e+00 y=0.000e+00
flux: x=0.000e+00 y=0.000e+00
System Analysis Report
=======================
Nodes:
---------------------
Node_224:
x: [0.000 0.000]
fix: ['T']
u: [0.000]
Node_225:
x: [2.000 0.000]
u: [2.000]
Node_226:
x: [4.000 0.000]
u: [4.000]
Node_227:
x: [6.000 0.000]
u: [6.000]
Node_228:
x: [8.000 0.000]
u: [8.000]
Node_229:
x: [10.000 0.000]
u: [10.000]
Node_230:
x: [0.000 1.000]
fix: ['T']
u: [0.000]
Node_231:
x: [2.000 1.000]
u: [2.000]
Node_232:
x: [4.000 1.000]
u: [4.000]
Node_233:
x: [6.000 1.000]
u: [6.000]
Node_234:
x: [8.000 1.000]
u: [8.000]
Node_235:
x: [10.000 1.000]
u: [10.000]
Elements:
---------------------
Triangle_341: nodes ( Node_224 Node_225 Node_230 )
material: Thermal
grad phi: x=1.000e+00 y=0.000e+00
flux: x=-1.000e+00 y=-0.000e+00
Triangle_342: nodes ( Node_231 Node_230 Node_225 )
material: Thermal
grad phi: x=1.000e+00 y=0.000e+00
flux: x=-1.000e+00 y=-0.000e+00
Triangle_343: nodes ( Node_225 Node_226 Node_231 )
material: Thermal
grad phi: x=1.000e+00 y=0.000e+00
flux: x=-1.000e+00 y=-0.000e+00
Triangle_344: nodes ( Node_232 Node_231 Node_226 )
material: Thermal
grad phi: x=1.000e+00 y=0.000e+00
flux: x=-1.000e+00 y=-0.000e+00
Triangle_345: nodes ( Node_226 Node_227 Node_232 )
material: Thermal
grad phi: x=1.000e+00 y=0.000e+00
flux: x=-1.000e+00 y=-0.000e+00
Triangle_346: nodes ( Node_233 Node_232 Node_227 )
material: Thermal
grad phi: x=1.000e+00 y=0.000e+00
flux: x=-1.000e+00 y=-0.000e+00
Triangle_347: nodes ( Node_227 Node_228 Node_233 )
material: Thermal
grad phi: x=1.000e+00 y=0.000e+00
flux: x=-1.000e+00 y=-0.000e+00
Triangle_348: nodes ( Node_234 Node_233 Node_228 )
material: Thermal
grad phi: x=1.000e+00 y=-8.882e-16
flux: x=-1.000e+00 y=8.882e-16
Triangle_349: nodes ( Node_228 Node_229 Node_234 )
material: Thermal
grad phi: x=1.000e+00 y=-8.882e-16
flux: x=-1.000e+00 y=8.882e-16
Triangle_350: nodes ( Node_235 Node_234 Node_229 )
material: Thermal
grad phi: x=1.000e+00 y=-1.776e-15
flux: x=-1.000e+00 y=1.776e-15
Total running time of the script: (0 minutes 0.575 seconds)