Bending a cantilever beam using a mixed mesh of Quad and Frame2D elements

• Using PatchMesher to model the 2d model portion

• Using Frame2D to model the beam/frame model portion

• Using BeamSolidLink to connect the two model types

Background Theory

This problem can be approximately validated using Bernoulli-Euler theory for small deformations. The given problem shall be modeled using

parameter	value	description
$E$		modulus of elasticity (in ksi)
$I$	666.667	area moment of inertia (in $inche{s}^4$)
$L$		length of the cantilever (in inches)
$P$		force at $x=L$ (in kips)

The general solution then yields

$$v(x)=-\frac{P{L}^3}{6EI}{\left(\frac{x}{L}\right)}^2(3-\frac{x}{L})$$

$$\theta (x)=\frac{d}{dx}v(x)=-\frac{P{L}^2}{2EI}\left(\frac{x}{L}\right)(2-\frac{x}{L})$$

$$M(x)=EI\frac{d}{dx}\theta (x)=-\frac{PL}{6}(1-\frac{x}{L})$$

$$V(x)=\frac{d}{dx}M(x)=P$$

For small displacement theory, the horizontal movement at the centerline is zero.

Reference values for a load factor of $\lambda =1.0$

variable	value	description
$u(L)$	0.000	end displacement (in inches). $u>0$ means moving to the right.
$v(L)$	-1.296	end displacement (in inches). $v>0$ means moving up.
$\theta (L)$	$-16.20\ast {10}^{-3}$	end displacement (in radians). $\theta >0$ means counter-clockwise rotation.

Reference values for a load factor of $\lambda =10.0$

variable	value	description
$u(L)$	0.000	end displacement (in inches). $u>0$ means moving to the right.
$v(L)$	-12.96	end displacement (in inches). $v>0$ means moving up.
$\theta (L)$	$-162.0\ast {10}^{-3}$	end displacement (in radians). $\theta >0$ means counter-clockwise rotation.

import numpy as np

from femedu.examples import Example

from femedu.domain import System, Node
from femedu.solver import NewtonRaphsonSolver
from femedu.elements.linear import Quad, Frame2D, BeamSolidLink
from femedu.materials import PlaneStress, ElasticSection
from femedu.mesher import PatchMesher, CurveMesher


class ExampleMixed10(Example):

    def problem(self):
        # ========== setting mesh parameters ==============

        Nx = 12  # number of elements in the mesh
        Ny = 8  # number of elements in the mesh
        Lx = 120.0  # length of plate in the x-direction
        Ly = 20.0  # length of plate in the y-direction

        # ========== setting material parameters ==============

        params2d = dict(
            E = 20000., # Young's modulus
            nu= 0.250,  # Poisson's ratio
            t =  1.00   # thickness of the plate
        )

        beamParams = dict(
            E = 20000.,    # Young's modulus
            A = Ly,        # cross section area
            I = Ly**3/12.  # cross section moment of inertia
        )

        # ========== setting load parameters ==============

        px = 0.0  # uniform load normal to x=Lx
        py = 0.0  # uniform load normal to y=Ly
        pxy = 1.5  # uniform shear load on x=L

        # ========== setting analysis parameters ==============

        target_load_level = 10.00  # reference load
        max_steps = 2  # number of load steps: 2 -> [0.0, 1.0]

        # define a list of target load levels
        load_levels = np.linspace(0, target_load_level, max_steps + 1)

        #
        # ==== Build the system model ====
        #

        model = System()
        model.setSolver(NewtonRaphsonSolver())

        # create the 2d portion
        mesher = PatchMesher(model, (0.,-Ly/2), (Lx/2,-Ly/2), (Lx/2, Ly/2), (0., Ly/2))
        nodes, quads = mesher.quadMesh(Nx, Ny, Quad, PlaneStress(params2d))

        # create a list of nodes on the interface
        # .. we do this before we create the frame elements
        # .. to avoid checking for the one frame node along that line
        section = model.findNodesAlongLine((Lx/2, 0.0), (0.0, 1.0))

        # create the beam portion
        frameMesher = CurveMesher(model, (Lx/2, 0.0), (Lx, 0.0))
        frameNodes, beams = frameMesher.lineMesh(Nx, Frame2D, ElasticSection(beamParams))

        # find the lead node
        for lead_node in frameNodes:
            if lead_node.isClose((Lx/2,0.0)):
                break

        # create the links
        for plate_node, _ in section:
            model.addElement(BeamSolidLink(lead_node, plate_node))

        # define support(s)

        ## find nodes at x==0
        for node, _ in model.findNodesAlongLine((0.0, 0.0), (0.0, 1.0)):
            node.fixDOF('ux', 'uy')

        # find the node on the beam axis (y==0.0) at the end of the beam (x==Lx)
        end_node, _ = model.findNodesAt((Lx, 0.0))[0]

        # ==== complete the reference load ====

        # the section at the right end (Frame model)
        # .. this must be the integral over the end section, i.e., traction multiplied by the height.
        end_node.setLoad([px * Ly, -pxy * Ly], ['ux', 'uy'])

        # surface loading on the top face
        # .. 2d portion
        for _, face in model.findFacesAlongLine((0.0, Ly), (1.0, 0.0), orientation=-1):
            face.setLoad(-py, 0.0)
        # .. frame portion
        for elem in beams:
            elem.setDistLoad(-py)

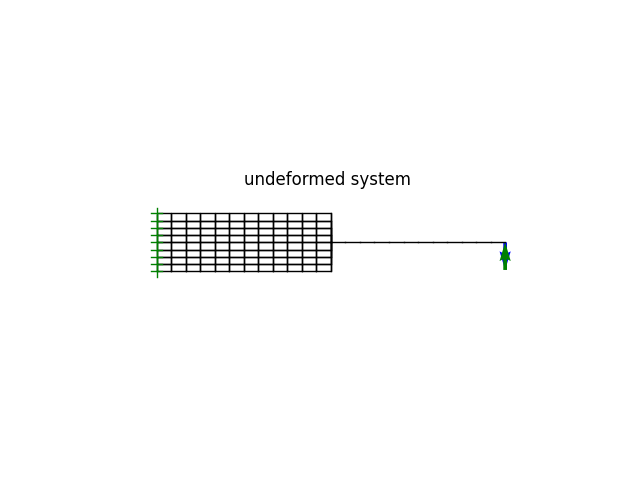
        model.plot(factor=0, title="undeformed system", show_bc=1, show_loads=1)

        for lf in load_levels:
            model.setLoadFactor(lf)
            model.solve(verbose=True)

        #model.report()

        model.plot(factor=1., show_bc=1, show_loads=1, show_reactions=1)

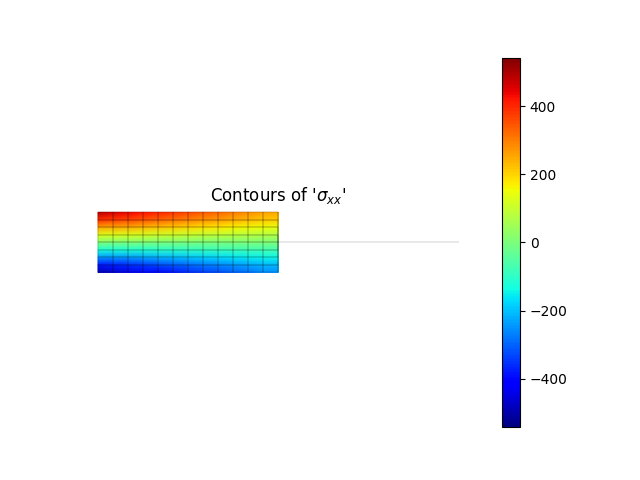
        model.valuePlot('sxx', show_mesh=True)
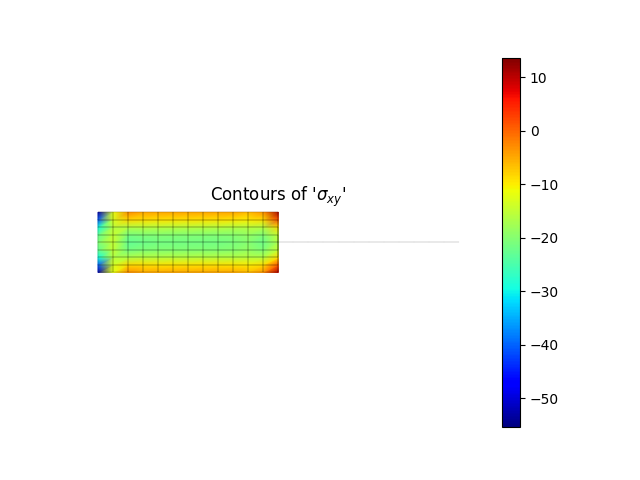
        model.valuePlot('sxy', show_mesh=True)
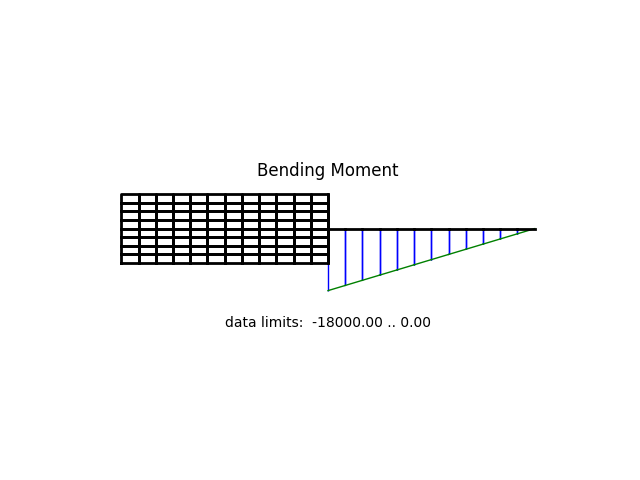
        model.beamValuePlot('M')
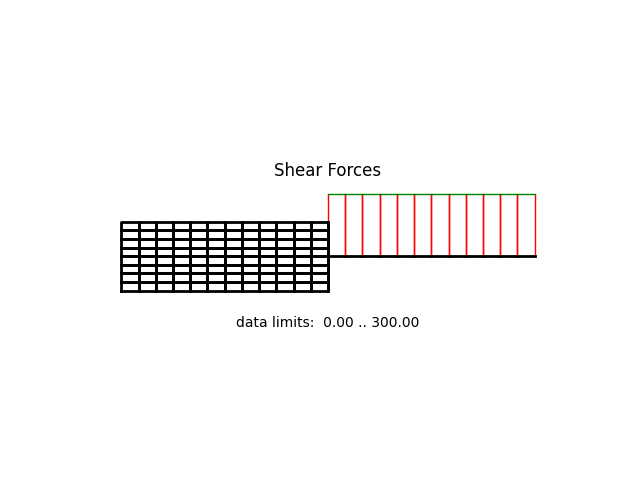
        model.beamValuePlot('V')

        msg = r"""
        The applied load at a load factor of 10.0 is:
          * horizontal force at the right end node:             {:8.3f} kips
          * vertical force at the right end node:               {:8.3f} kips
          * distributed vertical load along the upper boundary: {:8.5f} k/in

        The end deflection of the cantilever at this load is:
          * horizontal displacement: {:8.3f} in
          * vertical displacement:   {:8.3f} in
          * rotation (CCW): {:8.1f} * 10^-3 rad
        """.format(
            lf*px*Ly,
            lf*pxy*Ly,
            py,
            *end_node.getDisp(['ux','uy']),
            1.0e3*end_node.getDisp(['rz'])[0]
        )
        print(msg)

Run the example by creating an instance of the problem and executing it by calling Example.run()

if __name__ == "__main__":
    ex = ExampleMixed10()
    ex.run()

• 
• 
• 
• 
• 
• 

norm of the out-of-balance force:   4.9315e-10
+
norm of the out-of-balance force:   1.5000e+02
norm of the out-of-balance force:   7.3680e-09
+
norm of the out-of-balance force:   1.5000e+02
norm of the out-of-balance force:   1.4148e-08
+
/Users/pmackenz/Development/Educational/FEM.edu/src/femedu/elements/Element.py:350: UserWarning: ** WARNING ** Frame2D.mapGaussPoints not implemented
  warnings.warn(msg)
/Users/pmackenz/Development/Educational/FEM.edu/src/femedu/elements/Element.py:350: UserWarning: ** WARNING ** BeamSolidLink.mapGaussPoints not implemented
  warnings.warn(msg)
/Users/pmackenz/Development/Educational/FEM.edu/src/femedu/elements/Element.py:333: UserWarning: ** WARNING ** Quad.getInternalForce not implemented
  warnings.warn(msg)

        The applied load at a load factor of 10.0 is:
          * horizontal force at the right end node:                0.000 kips
          * vertical force at the right end node:                300.000 kips
          * distributed vertical load along the upper boundary:  0.00000 k/in

        The end deflection of the cantilever at this load is:
          * horizontal displacement:   -0.000 in
          * vertical displacement:    -12.749 in
          * rotation (CCW):   -158.4 * 10^-3 rad