A first 1D spring system with nicer plots

             o---/\/\/\---o---/\/\/\---o
x---/\/\/\---o                         o--->
             o-------/\/\/\/\/\--------o

x ... fixed node
o ... free node (moving in x-direction)

This problem is mechanically identical to A first 1D spring system but demonstrates the use of the leader-follower concept built into the Node class. We are using the concept to move springs apart in plots while maintaining the 1d kinematics.

Note

This example uses

• System class

• Spring class

• Node class

Initialization

from femedu.domain import *
from femedu.elements.linear import Spring

Building the model

1. Initializing a model

model = System()

2. Defining nodes

nd1  = Node(0.0, 0.0)
nd2  = Node(2.0, 0.0)
nd2a = Node(2.0, 1.0)
nd2b = Node(2.0,-1.0)
nd3  = Node(4.0, 1.0)
nd4  = Node(6.0, 0.0)
nd4a = Node(6.0, 1.0)
nd4b = Node(6.0,-1.0)

model.addNode(nd1, nd2, nd3, nd4)

nd2a.make_follower(nd2)
nd2b.make_follower(nd2)
nd4a.make_follower(nd4)
nd4b.make_follower(nd4)

3. Creating the springs

springA = Spring(nd1, nd2, 15)
springB = Spring(nd2a, nd3, 10)
springC = Spring(nd3, nd4a, 10)
springD = Spring(nd2b, nd4b, 10)

model.addElement(springA,springB,springC,springD)

4. Applying the essential boundary conditions

nd1.fixDOF('ux')

5. Applying loads

nd4.setLoad([2.0],['ux'])

You may check your model any time by executing

model.report()

System Analysis Report
=======================

Nodes:
---------------------
  Node_4:
      x:    [0. 0.]
      fix:  ['ux']
      u:    None
  Node_5:
      x:    [2. 0.]
      u:    None
  Node_8:
      x:    [4. 1.]
      u:    None
  Node_9:
      x:    [6. 0.]
      P:    [2.]
      u:    None

Elements:
---------------------
  Spring Elem_4: Node_4 to Node_5 with c=15
      length change:  delta = 0.0
      internal force: force = 0.0
  Spring Elem_5: Node_6 to Node_8 with c=10
      length change:  delta = 0.0
      internal force: force = 0.0
  Spring Elem_6: Node_8 to Node_10 with c=10
      length change:  delta = 0.0
      internal force: force = 0.0
  Spring Elem_7: Node_7 to Node_11 with c=10
      length change:  delta = 0.0
      internal force: force = 0.0

Performing the analysis

6. Assembly and solve

model.solve()

7. Check out displacements and internal forces

model.report()

System Analysis Report
=======================

Nodes:
---------------------
  Node_4:
      x:    [0. 0.]
      fix:  ['ux']
      u:    [0.]
  Node_5:
      x:    [2. 0.]
      u:    [0.13333333]
  Node_8:
      x:    [4. 1.]
      u:    [0.2]
  Node_9:
      x:    [6. 0.]
      P:    [2.]
      u:    [0.26666667]

Elements:
---------------------
  Spring Elem_4: Node_4 to Node_5 with c=15
      length change:  delta = 0.1333333333333333
      internal force: force = 1.9999999999999996
  Spring Elem_5: Node_6 to Node_8 with c=10
      length change:  delta = 0.06666666666666671
      internal force: force = 0.6666666666666671
  Spring Elem_6: Node_8 to Node_10 with c=10
      length change:  delta = 0.06666666666666665
      internal force: force = 0.6666666666666665
  Spring Elem_7: Node_7 to Node_11 with c=10
      length change:  delta = 0.13333333333333336
      internal force: force = 1.3333333333333335

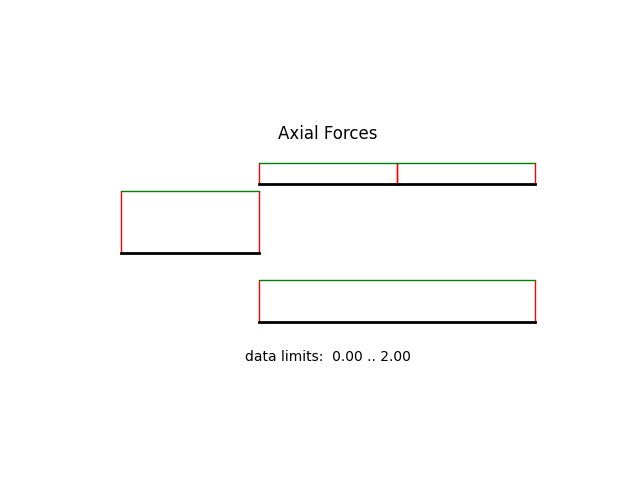
We can also create a force plot, though it doesn’t look all that nice in 1D

model.beamValuePlot('f')
model.plot(factor=10.0)

• 
•