Tutorial 3 - Loading a Model

This tutorial demonstrated loading techniques in FEM.edu.

The preparation stage

Before building a model, we need to load the used components. Every model needs one System instance. Furthermore, we are going to use several Node and Element instances.

from femedu.domain import System, Node
from femedu.elements.linear import Quad, Triangle
from femedu.materials import PlaneStress

# create a model domain
model = System()

Nodal loads

Depending on your model, these may be nodal forces, moments, or field values (e.g., temperature)

# create a node and add it to the model
node0 = Node(10., 2.)
model.addNode(node0)

# you need to create a mesh to such that your node learns about the available degrees of freedom
# ...
nd1 = Node(3., 5.)
nd2 = Node(0.,0.0)
model += nd1
model += nd2
model += Triangle(node0, nd1, nd2, PlaneStress())

Direct approach

If you create a node directly and, thus, have its handle available, you can load that node as follows.

apply a point load \(P_x = 3.14\) and \(P_y=-12.345\) driving dofs ‘ux’ and ‘uy’

node0.addLoad((3.14, -12.345), ('ux','uy'))

apply a moment \(M_z=20.0\) at the node. This moment drives a rotation ‘rz’, so we need to use that dof-indicator.

node0.addLoad((20.0,),('rz',))

Note

Both values and dof-indicators must be provided as a list. Python list-types list and tuple are accepts. When using tuple, as in the above example, you must not forget the extra comma (,) when creating a tuple containing just a single element. Alternatively, you may use a list as follows.

node0.addLoad([20.0],['rz'])

You may verify that your load has been properly recorded by printing the loaded node’s internal loads dictionary.

print(node0.loads)

model.plot(show_loads=1, show_reactions=0)

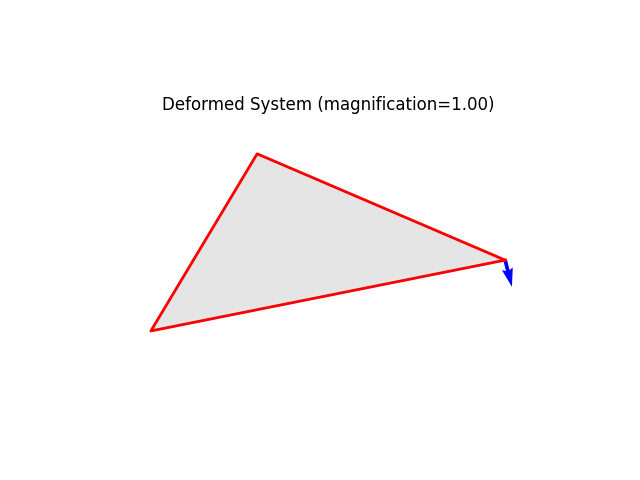
{'ux': 3.14, 'uy': -12.345, 'rz': 20.0}

Geometry-based loading

This approach is needed when a Mesher() was used to generate the finite element mesh. In that case, you can locate one or more node objects based on their location using

nodes = model.findNodesAt((3.,5.))

This function return a list of tuples containing a Node() object and its distance from the target point. If no nodes are found, an empty list is returned.

Since more than one node might be located, the user should check if

• any node was found: if nodes: ...

• more than one node has been found: if len(nodes) >1: ...

• or simply use the first node in that list: node_at_location, dist = nodes[0]

node_at_location, dist = nodes[0]
node_at_location.addLoad((30.0,),('ux',))
model.plot(show_loads=1, show_reactions=0)

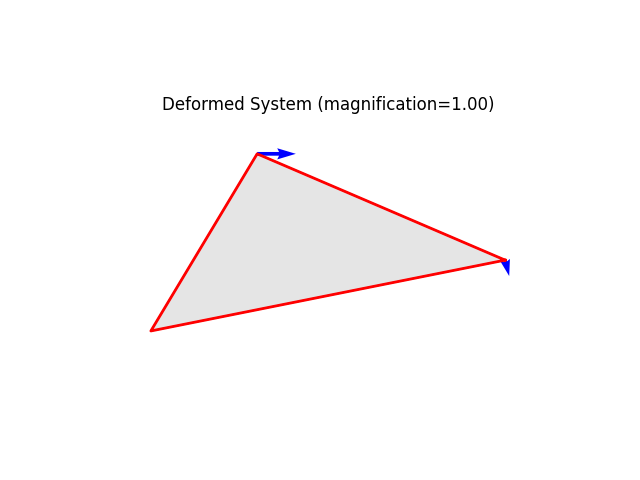
Note

Nodal loads are only applied to those degrees of freedom that are actually supported by the attached elements. Loads attached to dofs that are not part of the mechanical model are ignored.

Line loads

These are commonly used with beams and frames to represent axial and transverse distributed loads.

Face Loads in 2D

These represent distributed normal and shear loads along the edges of plates. To understand how those loads are applied within FEM.edu we need to know that each triangular or each quadrilateral element possesses three or four Face2D() objects, respectively. It is those objects that are handling user-provided distributed loads and converting them into nodal forces for the element.

Surface loads in 3D

These are not yet available in FEM.edu.