Example: plate03
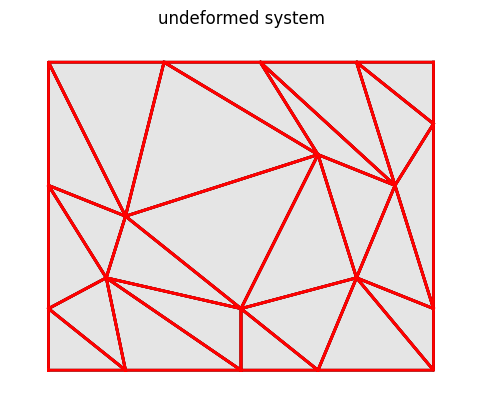
Initial system and meshing for the patch test.
We build the model based a few parameters as follows.
1 # ========== setting mesh parameters ==============
2
3 N = 8 # number of elements in the mesh
4 Lx = 100.0 # length of plate in the x-direction
5 Ly = 80.0 # length of plate in the y-direction
6
7 # ========== setting material parameters ==============
8
9 params = dict(
10 E = 20000., # Young's modulus
11 nu = 0.250, # Poisson's ratio
12 t = 1.00 # thickness of the plate
13 )
14
15 # ========== setting load parameters ==============
16
17 px = 10.0 # uniform load normal to x=const
18 py = 0.0 # uniform load normal to y=const
19 pxy = 0.0 # uniform shear load on x=const and y=const
20
21 # ========== setting analysis parameters ==============
22
23 target_load_level = 1.00 # reference load
24 max_steps = 2 # number of load steps: 2 -> [0.0, 1.0]
25
26 # define a list of target load levels
27 load_levels = np.linspace(0, target_load_level, max_steps)
Lines 26-27 define the list of target load levels for the nonlinear analysis. For the patch test, we actually need only a single non-zero load level, though more may be used for other purposes.
All mesh creation is based solely on the above parameters to allow for easy manipulation of the model.
The actual model is built by the block below.
28 #
29 # ==== Build the system model ====
30 #
31
32 model = System()
33 model.setSolver(NewtonRaphsonSolver())
34
35 # create nodes
36
37 nodes = (
38 Node(0.0*Lx, 0.0*Ly), # nd 0
39 Node(0.2*Lx, 0.0*Ly), # nd 1
40 Node(0.5*Lx, 0.0*Ly), # nd 2
41 Node(0.7*Lx, 0.0*Ly), # nd 3
42 Node(1.0*Lx, 0.0*Ly), # nd 4
43 #
44 Node(0.0*Lx, 0.2*Ly), # nd 5
45 Node(0.15*Lx,0.3*Ly), # nd 6
46 Node(0.5*Lx, 0.2*Ly), # nd 7
47 Node(0.8*Lx, 0.3*Ly), # nd 8
48 Node(1.0*Lx, 0.2*Ly), # nd 9
49 #
50 Node(0.0*Lx, 0.6*Ly), # nd 10
51 Node(0.2*Lx, 0.5*Ly), # nd 11
52 Node(0.7*Lx, 0.7*Ly), # nd 12
53 Node(0.9*Lx, 0.6*Ly), # nd 13
54 Node(1.0*Lx, 0.8*Ly), # nd 14
55 #
56 Node(0.0*Lx, 1.0*Ly), # nd 15
57 Node(0.3*Lx, 1.0*Ly), # nd 16
58 Node(0.55*Lx,1.0*Ly), # nd 17
59 Node(0.8*Lx, 1.0*Ly), # nd 18
60 Node(1.0*Lx, 1.0*Ly), # nd 19
61 )
62
63 elements = (
64 LinearTriangle(nodes[0],nodes[1],nodes[5],PlaneStress(params)), # elem 0
65 LinearTriangle(nodes[1],nodes[2],nodes[6],PlaneStress(params)), # elem 1
66 LinearTriangle(nodes[2],nodes[3],nodes[7],PlaneStress(params)), # elem 2
67 LinearTriangle(nodes[3],nodes[4],nodes[8],PlaneStress(params)), # elem 3
68 #
69 LinearTriangle(nodes[6],nodes[5],nodes[1],PlaneStress(params)), # elem 4
70 LinearTriangle(nodes[7],nodes[6],nodes[2],PlaneStress(params)), # elem 5
71 LinearTriangle(nodes[8],nodes[7],nodes[3],PlaneStress(params)), # elem 6
72 LinearTriangle(nodes[9],nodes[8],nodes[4],PlaneStress(params)), # elem 7
73 #
74 LinearTriangle(nodes[5],nodes[6],nodes[10],PlaneStress(params)), # elem 8
75 LinearTriangle(nodes[6],nodes[7],nodes[11],PlaneStress(params)), # elem 9
76 LinearTriangle(nodes[7],nodes[8],nodes[12],PlaneStress(params)), # elem 10
77 LinearTriangle(nodes[8],nodes[9],nodes[13],PlaneStress(params)), # elem 11
78 #
79 LinearTriangle(nodes[11],nodes[10],nodes[6],PlaneStress(params)), # elem 12
80 LinearTriangle(nodes[12],nodes[11],nodes[7],PlaneStress(params)), # elem 13
81 LinearTriangle(nodes[13],nodes[12],nodes[8],PlaneStress(params)), # elem 14
82 LinearTriangle(nodes[14],nodes[13],nodes[9],PlaneStress(params)), # elem 15
83 #
84 LinearTriangle(nodes[10],nodes[11],nodes[15],PlaneStress(params)), # elem 16
85 LinearTriangle(nodes[11],nodes[12],nodes[16],PlaneStress(params)), # elem 17
86 LinearTriangle(nodes[12],nodes[13],nodes[17],PlaneStress(params)), # elem 18
87 LinearTriangle(nodes[13],nodes[14],nodes[18],PlaneStress(params)), # elem 19
88 #
89 LinearTriangle(nodes[16],nodes[15],nodes[11],PlaneStress(params)), # elem 20
90 LinearTriangle(nodes[17],nodes[16],nodes[12],PlaneStress(params)), # elem 21
91 LinearTriangle(nodes[18],nodes[17],nodes[13],PlaneStress(params)), # elem 22
92 LinearTriangle(nodes[19],nodes[18],nodes[14],PlaneStress(params)), # elem 23
93 )
94
95 model.addNode(*nodes)
96 model.addElement(*elements)
Line 32 instantiates one model space.
Line 33 switches from the default linear solver to the NewtonRaphsonSolver, needed for nonlinear problems.
Lines 37-61 create the nodes, lines 63-93 create the elements and lines 95-96 adds them to the model space.
The patch test should be entirely load controlled and kinematic constraints shall be set to the absolute minimum: preventing a rigid body mode without ever imposing any constraints on deformation. The following lines represent such a minimum support.
97 # define support(s)
98
99 fix_x = (0,)
100 fix_y = (0,4)
101
102 for idx in fix_x:
103 nodes[idx].fixDOF('ux') # horizontal support left end
104 for idx in fix_y:
105 nodes[idx].fixDOF('uy') # vertical support right end
The load is applied as an equilibrium group, i.e., such that they do not generate any support reactions. A uniform horizontal tension is applied using surface loads.
106 # surface loads on the left side
107 elements[ 0].setSurfaceLoad(2,px)
108 elements[8].setSurfaceLoad(2,px)
109 elements[16].setSurfaceLoad(2,px)
110
111 # surface loads on the right side
112 elements[ 7].setSurfaceLoad(2,px)
113 elements[15].setSurfaceLoad(2,px)
114 elements[23].setSurfaceLoad(2,px)
See Example: plate02 for another, simpler example, and Triangle class for the definition of faces for this element.
The actual computation is as simple as a single call to the solver:
115 model.setLoadFactor(10.0)
116 model.solve()
You can obtain a debug-style report on the state of the system:
117 model.report()
The report will look something like this:
System Analysis Report ======================= Nodes: --------------------- Node_0: x: [0. 0.] fix: ['ux', 'uy'] u: [0. 0.] Node_1: x: [20. 0.] u: [9.92598389e-02 3.57659354e-16] Node_2: x: [50. 0.] u: [2.48149597e-01 7.56113665e-16] [ ... ] Elements: --------------------- LinearTriangle: nodes ( Node_0 Node_1 Node_5 ) material: PlaneStress strain: xx=4.975e-03 yy=-1.244e-03 xy=-6.038e-17 zz=-9.329e-04 stress: xx=9.951e+01 yy=2.959e-12 xy=-4.830e-13 zz=0.000e+00 element forces added to node: Node_0: [-800. 0.] Node_1: [0. 0.] Node_5: [-800. 0.] LinearTriangle: nodes ( Node_1 Node_2 Node_6 ) material: PlaneStress strain: xx=4.975e-03 yy=-1.244e-03 xy=-7.754e-17 zz=-9.329e-04 stress: xx=9.951e+01 yy=1.776e-12 xy=-6.203e-13 zz=0.000e+00 LinearTriangle: nodes ( Node_2 Node_3 Node_7 ) material: PlaneStress strain: xx=4.975e-03 yy=-1.244e-03 xy=2.659e-16 zz=-9.329e-04 stress: xx=9.951e+01 yy=6.516e-12 xy=2.127e-12 zz=0.000e+00 [ ... ]
A visual check, however, is usually more convenient.
118 model.plot(factor=10., filename="plate03_deformed.png")
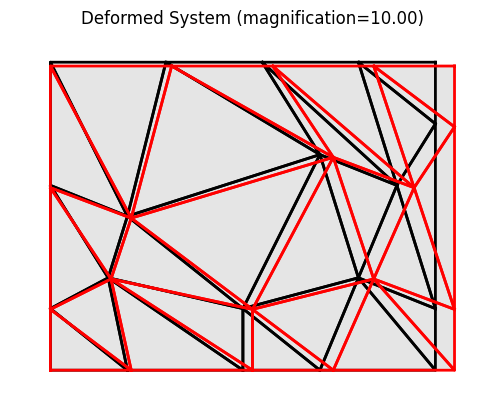
Deformed system at load level 1.00
Importing the example
from femedu.examples.plates.plate03 import *
# load the example
ex = ExamplePlate03()
More frame examples: Plate Examples