Buckling of a vertical beam with pin-pin support

modeled using a 2D frame element

|
| P
v
x o ... support
I
x   ... node
I
x   ... node
^   ... support

x ..... node
I ... frame element
<-- ... applied force
^ ..... pin support
o ..... roller support

degrees of freedom:
0 ... horizontal displacement
1 ... vertical displacement
2 ... rotation, theta

setting given parameters

N = 2	number of elements
L = 100.0	column length
EA = 2000000.0	axial stiffness
EI = 21000.0	flexural stiffness
w = 0.1	applied lateral load

Author: Peter Mackenzie-Helnwein

from femedu.examples.Example import *

from femedu.domain import *
from femedu.solver.NewtonRaphsonSolver import *
from femedu.elements.finite.Frame2D import *
from femedu.materials.ElasticSection import *


class ExampleFrame02(Example):

    def problem(self):
        # initialize a system model

        N  = 8     # number of elements
        L  = 100.0
        E  = 20000.
        EA = 2000000.0
        EI = 210000.0
        w  = -0.1

        params = {'E': E, 'A': EA/E, 'I': EI/E}

        model = System()
        model.setSolver(NewtonRaphsonSolver())

        # create nodes

        nd0 = Node(0.0, 0.0)
        model += nd0

        ndi = nd0
        for i in range(N):
            # nodes
            ndj = Node( 0.0, (i+1)*L/N )
            model += ndj

            # elements
            elem = Frame2D(ndi, ndj, ElasticSection(params))
            elem.setDistLoad(w)
            model += elem

            ndi = ndj

        # define support(s)
        nd0.fixDOF('ux', 'uy')    # horizontal and vertical support bottom end
        ndi.fixDOF('ux')          # horizontal support top end

        # add loads
        # .. load only the upper nodes
        Pcr = np.pi**2 * EI / L**2
        ndi.setLoad((-0.5*Pcr,), ('uy',))

        # show model information
        print(model)

        model.solve(verbose=True)

        model.report()

        model.plot(factor=10.0, filename="frame2_deformed.png")

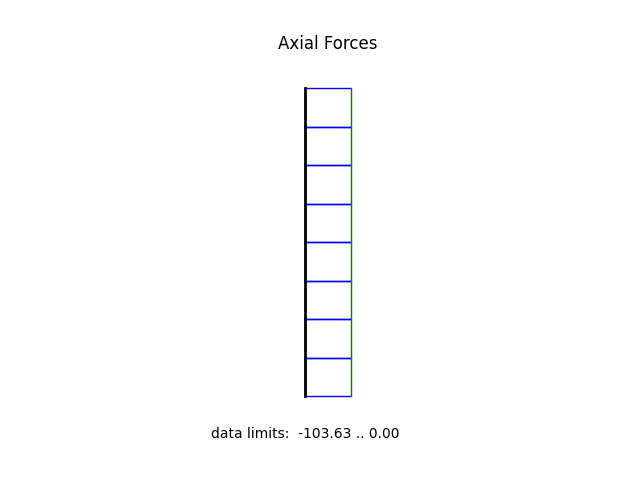
        model.beamValuePlot("F", filename="frame2_force.png")
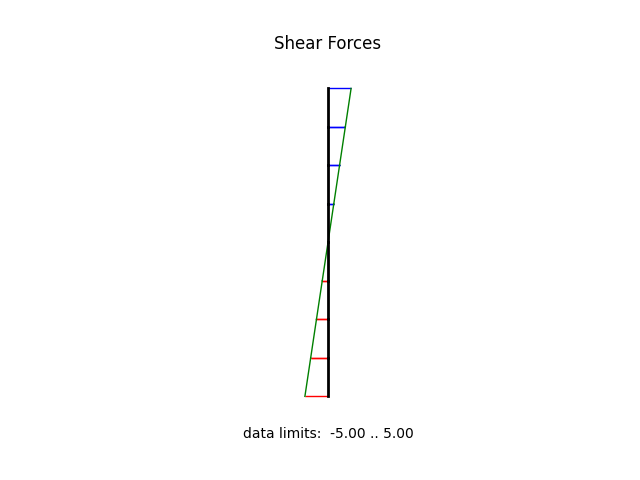
        model.beamValuePlot("V", filename="frame2_shear.png")
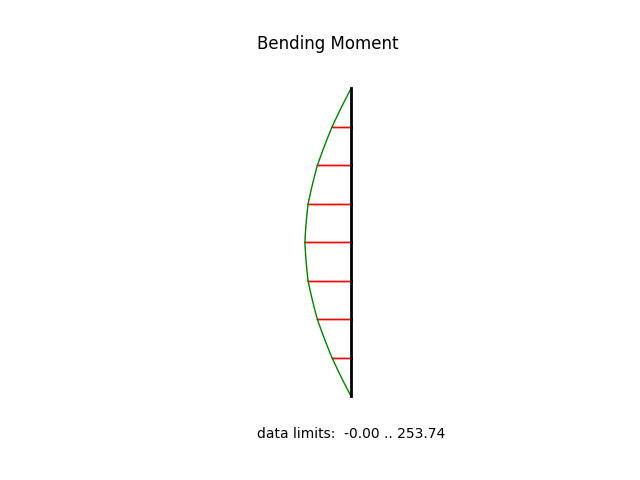
        model.beamValuePlot("M", filename="frame2_moment.png")

        return

Run the example by creating an instance of the problem and executing it by calling Example.run()

if __name__ == "__main__":
    ex = ExampleFrame02()
    ex.run()

• 
• 
• 
• 

System object
Node_186(x=[0. 0.], u=None)
Node_187(x=[ 0.  12.5], u=None)
Node_188(x=[ 0. 25.], u=None)
Node_189(x=[ 0.  37.5], u=None)
Node_190(x=[ 0. 50.], u=None)
Node_191(x=[ 0.  62.5], u=None)
Node_192(x=[ 0. 75.], u=None)
Node_193(x=[ 0.  87.5], u=None)
Node_194(x=[  0. 100.], u=None)
Frame2D(Node_186, Node_187, ElasticSection(Material)({'E': 20000.0, 'A': 100.0, 'I': 10.5, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_187, Node_188, ElasticSection(Material)({'E': 20000.0, 'A': 100.0, 'I': 10.5, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_188, Node_189, ElasticSection(Material)({'E': 20000.0, 'A': 100.0, 'I': 10.5, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_189, Node_190, ElasticSection(Material)({'E': 20000.0, 'A': 100.0, 'I': 10.5, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_190, Node_191, ElasticSection(Material)({'E': 20000.0, 'A': 100.0, 'I': 10.5, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_191, Node_192, ElasticSection(Material)({'E': 20000.0, 'A': 100.0, 'I': 10.5, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_192, Node_193, ElasticSection(Material)({'E': 20000.0, 'A': 100.0, 'I': 10.5, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_193, Node_194, ElasticSection(Material)({'E': 20000.0, 'A': 100.0, 'I': 10.5, 'nu': 0.0, 'fy': 1e+30}))
norm of the out-of-balance force:   1.0370e+02
norm of the out-of-balance force:   1.6462e+00
norm of the out-of-balance force:   1.5379e-10
+

System Analysis Report
=======================

Nodes:
---------------------
  Node_186:
      x:    [0. 0.]
      fix:  ['ux', 'uy']
      u:    [ 0.          0.         -0.03940975]
  Node_187:
      x:    [ 0.  12.5]
      u:    [ 0.47907861 -0.00064769 -0.03620643]
  Node_188:
      x:    [ 0. 25.]
      u:    [ 0.88199225 -0.00129539 -0.02745697]
  Node_189:
      x:    [ 0.  37.5]
      u:    [ 1.14899475 -0.00194308 -0.01475577]
  Node_190:
      x:    [ 0. 50.]
      u:    [ 1.24230366e+00 -2.59077116e-03  4.18404301e-15]
  Node_191:
      x:    [ 0.  62.5]
      u:    [ 1.14899475 -0.00323846  0.01475577]
  Node_192:
      x:    [ 0. 75.]
      u:    [ 0.88199225 -0.00388616  0.02745697]
  Node_193:
      x:    [ 0.  87.5]
      u:    [ 0.47907861 -0.00453385  0.03620643]
  Node_194:
      x:    [  0. 100.]
      fix:  ['ux']
      P:    [   0.         -103.63084621    0.        ]
      u:    [ 0.         -0.00518154  0.03940975]

Elements:
---------------------
  Frame2D_298: nodes ( Node_186 Node_187 )
      material: ElasticSection
      internal forces: f0=-103.63 V0=4.37 M0=1.30 fl=-103.63 Vl=4.37 Ml=105.64 Pw=-0.62 Mw=-1.30
  Frame2D_299: nodes ( Node_187 Node_188 )
      material: ElasticSection
      internal forces: f0=-103.63 V0=3.12 M0=105.64 fl=-103.63 Vl=3.12 Ml=186.45 Pw=-0.62 Mw=-1.30
  Frame2D_300: nodes ( Node_188 Node_189 )
      material: ElasticSection
      internal forces: f0=-103.63 V0=1.87 M0=186.45 fl=-103.63 Vl=1.87 Ml=237.56 Pw=-0.62 Mw=-1.30
  Frame2D_301: nodes ( Node_189 Node_190 )
      material: ElasticSection
      internal forces: f0=-103.63 V0=0.62 M0=237.56 fl=-103.63 Vl=0.62 Ml=255.04 Pw=-0.62 Mw=-1.30
  Frame2D_302: nodes ( Node_190 Node_191 )
      material: ElasticSection
      internal forces: f0=-103.63 V0=-0.63 M0=255.04 fl=-103.63 Vl=-0.63 Ml=237.56 Pw=-0.62 Mw=-1.30
  Frame2D_303: nodes ( Node_191 Node_192 )
      material: ElasticSection
      internal forces: f0=-103.63 V0=-1.88 M0=237.56 fl=-103.63 Vl=-1.88 Ml=186.45 Pw=-0.62 Mw=-1.30
  Frame2D_304: nodes ( Node_192 Node_193 )
      material: ElasticSection
      internal forces: f0=-103.63 V0=-3.13 M0=186.45 fl=-103.63 Vl=-3.13 Ml=105.64 Pw=-0.62 Mw=-1.30
  Frame2D_305: nodes ( Node_193 Node_194 )
      material: ElasticSection
      internal forces: f0=-103.63 V0=-4.38 M0=105.64 fl=-103.63 Vl=-4.38 Ml=1.30 Pw=-0.62 Mw=-1.30