Note
Go to the end to download the full example code.
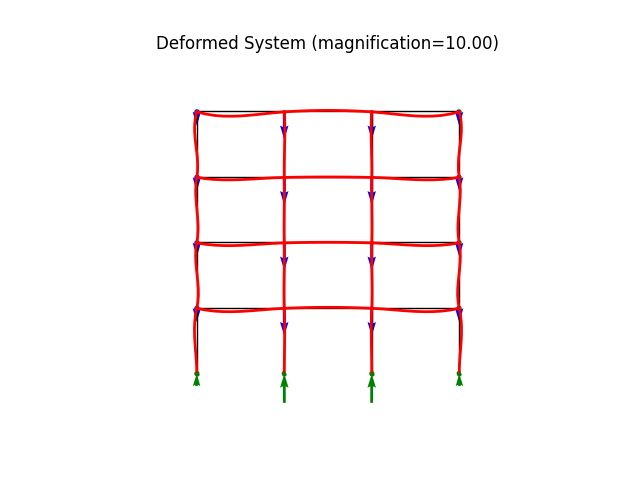
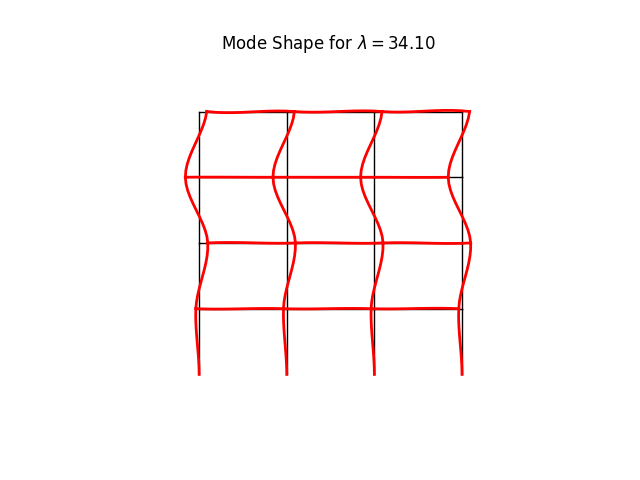
Buckling of a building frame
modeled using a 2D frame element
N = 2 |
number of elements |
L = 100.0 |
column length |
EA = 2000000.0 |
axial stiffness |
EI = 21000.0 |
flexural stiffness |
w = 0.1 |
applied lateral load |
Author: Peter Mackenzie-Helnwein
from femedu.examples.Example import *
from femedu.domain import *
from femedu.solver.NewtonRaphsonSolver import *
from femedu.elements.finite.Frame2D import *
from femedu.materials.ElasticSection import *
class ExampleFrame05(Example):
def problem(self):
# initialize a system model
N = 8 # number of elements
B = 720.
H = 720.
E = 29000.0
A = 150.0
I = 250.0
w = 0.10
load_at_nodes_only = False # set to True to apply equivalent nodal forces and moments
Ph = 0.01 # additional horizontal load per floor
Ph = 0.10 # additional horizontal load per floor
Ph = 1.00 # additional horizontal load per floor
Ph = 0.00 # additional horizontal load per floor
# ========== setting global parameters ==============
target_load_level = 33.
max_steps = 10
load_levels = np.linspace(0, target_load_level, max_steps)
# ========= build your structural model =============
model = System()
model.setSolver(NewtonRaphsonSolver())
x0 = 0.0
x1 = B / 3
x2 = 2 * B / 3
x3 = B
y0 = 0.0
y1 = H / 4
y2 = 2 * H / 4
y3 = 3 * H / 4
y4 = H
X10 = Node(x0, y0)
X11 = Node(x0, y1)
X12 = Node(x0, y2)
X13 = Node(x0, y3)
X14 = Node(x0, y4)
X20 = Node(x1, y0)
X21 = Node(x1, y1)
X22 = Node(x1, y2)
X23 = Node(x1, y3)
X24 = Node(x1, y4)
X30 = Node(x2, y0)
X31 = Node(x2, y1)
X32 = Node(x2, y2)
X33 = Node(x2, y3)
X34 = Node(x2, y4)
X40 = Node(x3, y0)
X41 = Node(x3, y1)
X42 = Node(x3, y2)
X43 = Node(x3, y3)
X44 = Node(x3, y4)
model.addNode(X10, X11, X12, X13, X14)
model.addNode(X20, X21, X22, X23, X24)
model.addNode(X30, X31, X32, X33, X34)
model.addNode(X40, X41, X42, X43, X44)
# columns
params = {'E': E, 'A': A, 'I': I}
C11 = Frame2D(X10, X11, ElasticSection(params))
C12 = Frame2D(X11, X12, ElasticSection(params))
C13 = Frame2D(X12, X13, ElasticSection(params))
C14 = Frame2D(X13, X14, ElasticSection(params))
model.addElement(C11, C12, C13, C14)
params = {'E': E, 'A': 2 * A, 'I': 1.5 * I}
C21 = Frame2D(X20, X21, ElasticSection(params))
C22 = Frame2D(X21, X22, ElasticSection(params))
C23 = Frame2D(X22, X23, ElasticSection(params))
C24 = Frame2D(X23, X24, ElasticSection(params))
model.addElement(C21, C22, C23, C24)
C31 = Frame2D(X30, X31, ElasticSection(params))
C32 = Frame2D(X31, X32, ElasticSection(params))
C33 = Frame2D(X32, X33, ElasticSection(params))
C34 = Frame2D(X33, X34, ElasticSection(params))
model.addElement(C31, C32, C33, C34)
params = {'E': E, 'A': A, 'I': I}
C41 = Frame2D(X40, X41, ElasticSection(params))
C42 = Frame2D(X41, X42, ElasticSection(params))
C43 = Frame2D(X42, X43, ElasticSection(params))
C44 = Frame2D(X43, X44, ElasticSection(params))
model.addElement(C41, C42, C43, C44)
# floors
params = {'E': E, 'A': A, 'I': 3 * I}
F11 = Frame2D(X11, X21, ElasticSection(params))
F12 = Frame2D(X21, X31, ElasticSection(params))
F13 = Frame2D(X31, X41, ElasticSection(params))
model.addElement(F11, F12, F13)
F21 = Frame2D(X12, X22, ElasticSection(params))
F22 = Frame2D(X22, X32, ElasticSection(params))
F23 = Frame2D(X32, X42, ElasticSection(params))
model.addElement(F21, F22, F23)
F31 = Frame2D(X13, X23, ElasticSection(params))
F32 = Frame2D(X23, X33, ElasticSection(params))
F33 = Frame2D(X33, X43, ElasticSection(params))
model.addElement(F31, F32, F33)
F41 = Frame2D(X14, X24, ElasticSection(params))
F42 = Frame2D(X24, X34, ElasticSection(params))
F43 = Frame2D(X34, X44, ElasticSection(params))
model.addElement(F41, F42, F43)
# fixities
X10.fixDOF('ux', 'uy', 'rz') # fixed
X20.fixDOF('ux', 'uy', 'rz') # fixed
X30.fixDOF('ux', 'uy', 'rz') # fixed
X40.fixDOF('ux', 'uy', 'rz') # fixed
# reference load
# Pcr = np.pi**2 * EI / L**2
model.resetLoad() # size load vector and initialize
# model.addLoad(Xn, -Pcr, dof=0) # add a horizontal force (first dof only) ; remember C-style indexing: 0,1,...,(n-1)
if load_at_nodes_only:
# floor loading as nodal loads ...
Pe = w * B / 3
Mi = w * (B / 3) ** 2 / 12
X11.addLoad([-Pe / 2., -Mi], ['uy', 'rz'])
X21.addLoad([-Pe / 2., 0.], ['uy', 'rz'])
X31.addLoad([-Pe / 2., 0.], ['uy', 'rz'])
X41.addLoad([-Pe / 2., Mi], ['uy', 'rz'])
X12.addLoad([-Pe / 2., -Mi], ['uy', 'rz'])
X22.addLoad([-Pe / 2., 0.], ['uy', 'rz'])
X32.addLoad([-Pe / 2., 0.], ['uy', 'rz'])
X42.addLoad([-Pe / 2., Mi], ['uy', 'rz'])
X13.addLoad([-Pe / 2., -Mi], ['uy', 'rz'])
X23.addLoad([-Pe / 2., 0.], ['uy', 'rz'])
X33.addLoad([-Pe / 2., 0.], ['uy', 'rz'])
X43.addLoad([-Pe / 2., Mi], ['uy', 'rz'])
X14.addLoad([-Pe / 2., -Mi], ['uy', 'rz'])
X24.addLoad([-Pe / 2., 0.], ['uy', 'rz'])
X34.addLoad([-Pe / 2., 0.], ['uy', 'rz'])
X44.addLoad([-Pe / 2., Mi], ['uy', 'rz'])
else:
# floor loading as distributed loads ...
F11.setDistLoad(-w)
F12.setDistLoad(-w)
F13.setDistLoad(-w)
F21.setDistLoad(-w)
F22.setDistLoad(-w)
F23.setDistLoad(-w)
F31.setDistLoad(-w)
F32.setDistLoad(-w)
F33.setDistLoad(-w)
F41.setDistLoad(-w)
F42.setDistLoad(-w)
F43.setDistLoad(-w)
# wind load ...
X11.addLoad([Ph], ['ux']) # horizontal load
X12.addLoad([Ph], ['ux']) # horizontal load
X13.addLoad([Ph], ['ux']) # horizontal load
X14.addLoad([Ph / 2], ['ux']) # horizontal load
# show model information
print(model)
print("\n==== perform the analysis ===\n")
# * apply the load in multiple smaller load steps
# set up data recorder
model.initRecorder()
model.trackStability(True)
# initialize the analysis:
model.resetDisplacements() # set U to all zeros
model.setLoadFactor(0.0) # define a known equilibrium solution
model.startRecorder()
detKt = []
lambdas = []
# solve for all load_levels
for loadfactor in load_levels:
# define node X2 as the controled node; downward direction is prescribed:
model.setLoadFactor(loadfactor)
model.solve(verbose=True)
# stability check
lambdas.append(model.loadfactor)
detKt.append(model.solver.checkStability())
# report results
print('+')
# model.report()
print("\n=== next load level ===\n")
#
# ==== create some nice plots ===
#
model.report()
model.plot(factor=10.0, filename="frame5_deformed.png", show_bc=1)
fig, ax = plt.subplots()
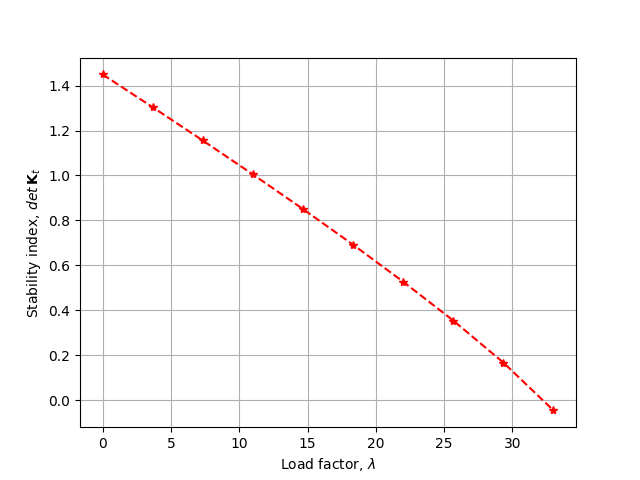
ax.plot(lambdas, detKt, '--*r')
ax.grid(True)
ax.set_xlabel('Load factor, $ \\lambda $')
ax.set_ylabel("Stability index, $ {det}\\: {\\bf K}_t $")
fig.savefig("frame5_stability.png")
fig.show()
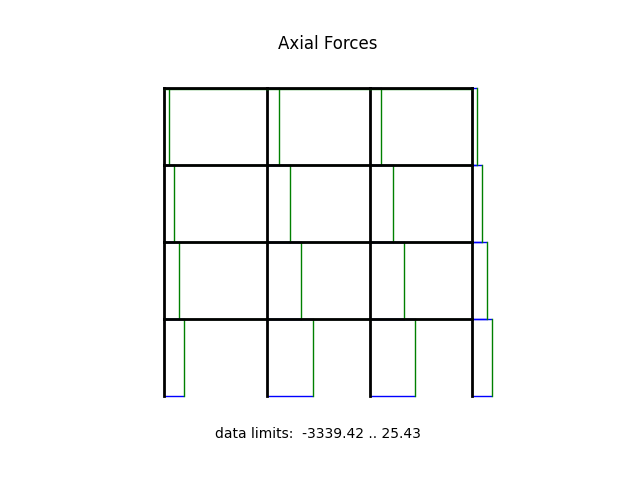
model.beamValuePlot("F", filename="frame5_force.png")
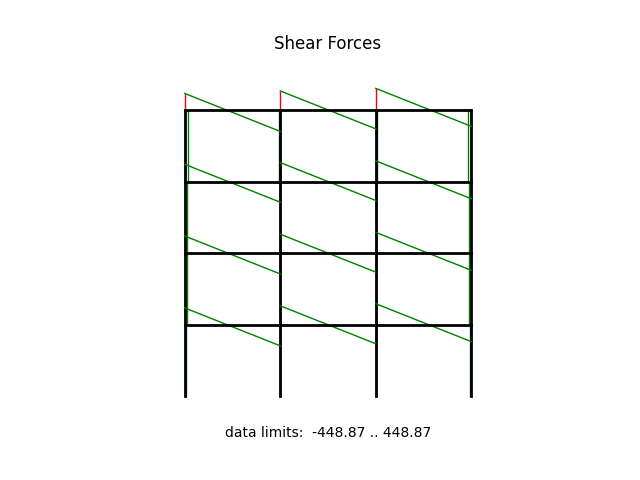
model.beamValuePlot("V", filename="frame5_shear.png")
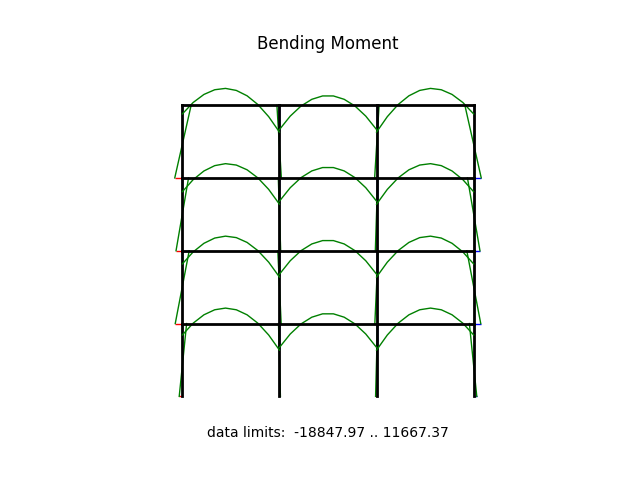
model.beamValuePlot("M", filename="frame5_moment.png")
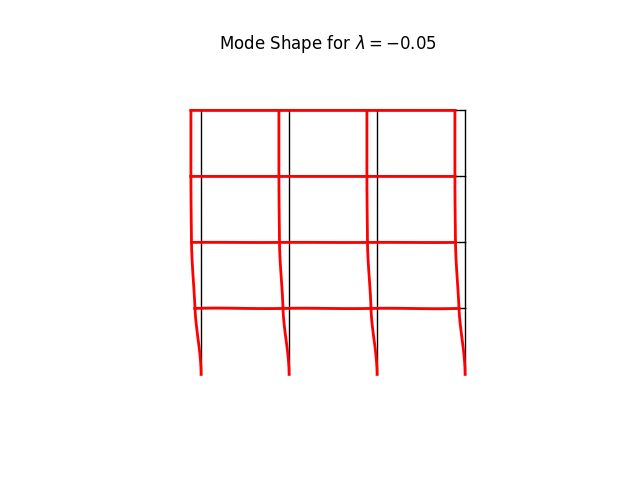
model.plotBucklingMode(factor=100., mode=0, filename="frame5_buckling_mode0.png")
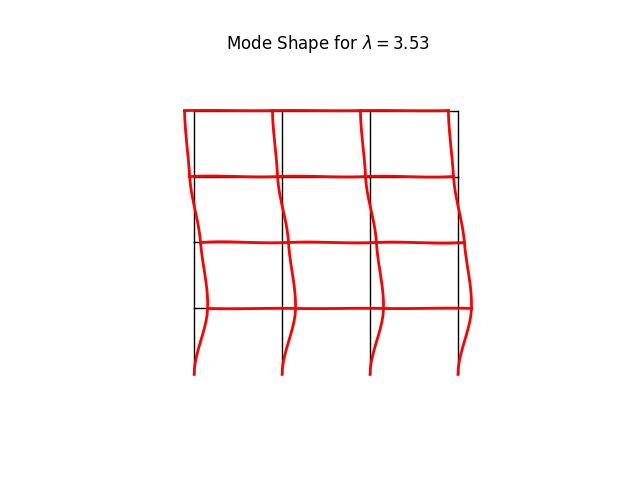
model.plotBucklingMode(factor=100., mode=1, filename="frame5_buckling_mode1.png")
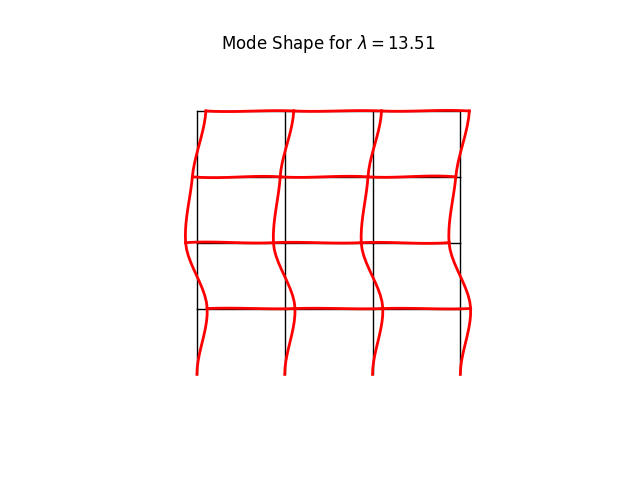
model.plotBucklingMode(factor=100., mode=2, filename="frame5_buckling_mode2.png")
model.plotBucklingMode(factor=100., mode=3, filename="frame5_buckling_mode3.png")
Run the example by creating an instance of the problem and executing it by calling Example.run()
if __name__ == "__main__":
ex = ExampleFrame05()
ex.run()
System object
Node_204(x=[0 0], u=None)
Node_205(x=[0 180], u=None)
Node_206(x=[0 360], u=None)
Node_207(x=[0 540], u=None)
Node_208(x=[0 720], u=None)
Node_209(x=[240 0], u=None)
Node_210(x=[240 180], u=None)
Node_211(x=[240 360], u=None)
Node_212(x=[240 540], u=None)
Node_213(x=[240 720], u=None)
Node_214(x=[480 0], u=None)
Node_215(x=[480 180], u=None)
Node_216(x=[480 360], u=None)
Node_217(x=[480 540], u=None)
Node_218(x=[480 720], u=None)
Node_219(x=[720 0], u=None)
Node_220(x=[720 180], u=None)
Node_221(x=[720 360], u=None)
Node_222(x=[720 540], u=None)
Node_223(x=[720 720], u=None)
Frame2D(Node_204, Node_205, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 250.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_205, Node_206, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 250.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_206, Node_207, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 250.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_207, Node_208, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 250.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_209, Node_210, ElasticSection(Material)({'E': 29000.0, 'A': 300.0, 'I': 375.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_210, Node_211, ElasticSection(Material)({'E': 29000.0, 'A': 300.0, 'I': 375.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_211, Node_212, ElasticSection(Material)({'E': 29000.0, 'A': 300.0, 'I': 375.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_212, Node_213, ElasticSection(Material)({'E': 29000.0, 'A': 300.0, 'I': 375.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_214, Node_215, ElasticSection(Material)({'E': 29000.0, 'A': 300.0, 'I': 375.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_215, Node_216, ElasticSection(Material)({'E': 29000.0, 'A': 300.0, 'I': 375.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_216, Node_217, ElasticSection(Material)({'E': 29000.0, 'A': 300.0, 'I': 375.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_217, Node_218, ElasticSection(Material)({'E': 29000.0, 'A': 300.0, 'I': 375.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_219, Node_220, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 250.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_220, Node_221, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 250.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_221, Node_222, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 250.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_222, Node_223, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 250.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_205, Node_210, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 750.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_210, Node_215, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 750.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_215, Node_220, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 750.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_206, Node_211, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 750.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_211, Node_216, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 750.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_216, Node_221, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 750.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_207, Node_212, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 750.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_212, Node_217, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 750.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_217, Node_222, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 750.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_208, Node_213, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 750.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_213, Node_218, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 750.0, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_218, Node_223, ElasticSection(Material)({'E': 29000.0, 'A': 150.0, 'I': 750.0, 'nu': 0.0, 'fy': 1e+30}))
==== perform the analysis ===
norm of the out-of-balance force: 0.0000e+00
** Stability check: (smallest 1 eigenvalues of Kt)
mode 0: 1.45
+
** Stability check: (smallest eigenvalue of Kt) = 1.4498657937285275
+
=== next load level ===
norm of the out-of-balance force: 4.9858e+03
norm of the out-of-balance force: 2.5683e+01
norm of the out-of-balance force: 6.8710e-03
norm of the out-of-balance force: 2.4430e-06
norm of the out-of-balance force: 1.6512e-07
** Stability check: (smallest 1 eigenvalues of Kt)
mode 0: 1.30
+
** Stability check: (smallest eigenvalue of Kt) = 1.3039606866245097
+
=== next load level ===
norm of the out-of-balance force: 4.9858e+03
norm of the out-of-balance force: 5.2545e+01
norm of the out-of-balance force: 2.8485e-02
norm of the out-of-balance force: 2.0784e-05
norm of the out-of-balance force: 7.0993e-08
** Stability check: (smallest 1 eigenvalues of Kt)
mode 0: 1.16
+
** Stability check: (smallest eigenvalue of Kt) = 1.1558244386254235
+
=== next load level ===
norm of the out-of-balance force: 4.9858e+03
norm of the out-of-balance force: 8.0699e+01
norm of the out-of-balance force: 6.6491e-02
norm of the out-of-balance force: 7.4326e-05
norm of the out-of-balance force: 7.1854e-08
** Stability check: (smallest 1 eigenvalues of Kt)
mode 0: 1.00
+
** Stability check: (smallest eigenvalue of Kt) = 1.0049715576213192
+
=== next load level ===
norm of the out-of-balance force: 4.9858e+03
norm of the out-of-balance force: 1.1028e+02
norm of the out-of-balance force: 1.2275e-01
norm of the out-of-balance force: 1.8726e-04
norm of the out-of-balance force: 2.5030e-07
** Stability check: (smallest 1 eigenvalues of Kt)
mode 0: 0.85
+
** Stability check: (smallest eigenvalue of Kt) = 0.8507250234763356
+
=== next load level ===
norm of the out-of-balance force: 4.9858e+03
norm of the out-of-balance force: 1.4143e+02
norm of the out-of-balance force: 1.9938e-01
norm of the out-of-balance force: 3.8921e-04
norm of the out-of-balance force: 6.6359e-07
** Stability check: (smallest 1 eigenvalues of Kt)
mode 0: 0.69
+
** Stability check: (smallest eigenvalue of Kt) = 0.6920949784275
+
=== next load level ===
norm of the out-of-balance force: 4.9858e+03
norm of the out-of-balance force: 1.7435e+02
norm of the out-of-balance force: 2.9877e-01
norm of the out-of-balance force: 7.1689e-04
norm of the out-of-balance force: 1.5020e-06
norm of the out-of-balance force: 1.3625e-08
** Stability check: (smallest 1 eigenvalues of Kt)
mode 0: 0.53
+
** Stability check: (smallest eigenvalue of Kt) = 0.5275391348656064
+
=== next load level ===
norm of the out-of-balance force: 4.9858e+03
norm of the out-of-balance force: 2.0925e+02
norm of the out-of-balance force: 4.2361e-01
norm of the out-of-balance force: 1.2154e-03
norm of the out-of-balance force: 3.0769e-06
norm of the out-of-balance force: 2.8825e-08
** Stability check: (smallest 1 eigenvalues of Kt)
mode 0: 0.35
+
** Stability check: (smallest eigenvalue of Kt) = 0.35442857202021694
+
=== next load level ===
norm of the out-of-balance force: 4.9858e+03
norm of the out-of-balance force: 2.4638e+02
norm of the out-of-balance force: 5.7696e-01
norm of the out-of-balance force: 1.9401e-03
norm of the out-of-balance force: 5.8237e-06
norm of the out-of-balance force: 2.2737e-08
** Stability check: (smallest 1 eigenvalues of Kt)
mode 0: 0.17
+
** Stability check: (smallest eigenvalue of Kt) = 0.1676343891118212
+
=== next load level ===
norm of the out-of-balance force: 4.9858e+03
norm of the out-of-balance force: 2.8607e+02
norm of the out-of-balance force: 7.6225e-01
norm of the out-of-balance force: 2.9585e-03
norm of the out-of-balance force: 1.0392e-05
norm of the out-of-balance force: 3.3931e-08
** Stability check: (smallest 1 eigenvalues of Kt)
mode 0: -0.05
+
** Stability check: (smallest eigenvalue of Kt) = -0.04529626517253338
+
=== next load level ===
System Analysis Report
=======================
Nodes:
---------------------
Node_204:
x: [0.000 0.000]
fix: ['ux', 'uy', 'rz']
u: [0.000 0.000 0.000]
Node_205:
x: [0.000 180.000]
u: [-0.002 -0.058 -0.024]
Node_206:
x: [0.000 360.000]
u: [0.000 -0.102 -0.020]
Node_207:
x: [0.000 540.000]
u: [-0.001 -0.131 -0.018]
Node_208:
x: [0.000 720.000]
u: [0.005 -0.146 -0.030]
Node_209:
x: [240.000 0.000]
fix: ['ux', 'uy', 'rz']
u: [0.000 0.000 0.000]
Node_210:
x: [240.000 180.000]
u: [-0.001 -0.069 0.005]
Node_211:
x: [240.000 360.000]
u: [0.000 -0.121 0.003]
Node_212:
x: [240.000 540.000]
u: [-0.000 -0.156 0.002]
Node_213:
x: [240.000 720.000]
u: [0.001 -0.173 0.007]
Node_214:
x: [480.000 0.000]
fix: ['ux', 'uy', 'rz']
u: [0.000 0.000 0.000]
Node_215:
x: [480.000 180.000]
u: [0.001 -0.069 -0.005]
Node_216:
x: [480.000 360.000]
u: [-0.000 -0.121 -0.003]
Node_217:
x: [480.000 540.000]
u: [0.000 -0.156 -0.002]
Node_218:
x: [480.000 720.000]
u: [-0.001 -0.173 -0.007]
Node_219:
x: [720.000 0.000]
fix: ['ux', 'uy', 'rz']
u: [0.000 0.000 0.000]
Node_220:
x: [720.000 180.000]
u: [0.002 -0.058 0.024]
Node_221:
x: [720.000 360.000]
u: [-0.000 -0.102 0.020]
Node_222:
x: [720.000 540.000]
u: [0.001 -0.131 0.018]
Node_223:
x: [720.000 720.000]
u: [-0.005 -0.146 0.030]
Elements:
---------------------
Frame2D_313: nodes ( Node_204 Node_205 )
material: ElasticSection
internal forces: f0=-1412.58 V0=-28.72 M0=2190.63 fl=-1412.58 Vl=-28.72 Ml=-2981.99 Pw=0.00 Mw=0.00
Frame2D_314: nodes ( Node_205 Node_206 )
material: ElasticSection
internal forces: f0=-1060.65 V0=-54.15 M0=4967.18 fl=-1060.65 Vl=-54.15 Ml=-4777.61 Pw=0.00 Mw=0.00
Frame2D_315: nodes ( Node_206 Node_207 )
material: ElasticSection
internal forces: f0=-702.83 V0=-48.56 M0=4417.41 fl=-702.83 Vl=-48.56 Ml=-4323.51 Pw=0.00 Mw=0.00
Frame2D_316: nodes ( Node_207 Node_208 )
material: ElasticSection
internal forces: f0=-343.13 V0=-63.72 M0=5307.41 fl=-343.13 Vl=-63.72 Ml=-6160.35 Pw=0.00 Mw=0.00
Frame2D_317: nodes ( Node_209 Node_210 )
material: ElasticSection
internal forces: f0=-3339.42 V0=7.47 M0=-673.83 fl=-3339.42 Vl=7.47 Ml=668.39 Pw=0.00 Mw=0.00
Frame2D_318: nodes ( Node_210 Node_211 )
material: ElasticSection
internal forces: f0=-2503.35 V0=12.97 M0=-1196.02 fl=-2503.35 Vl=12.97 Ml=1140.41 Pw=0.00 Mw=0.00
Frame2D_319: nodes ( Node_211 Node_212 )
material: ElasticSection
internal forces: f0=-1673.17 V0=9.16 M0=-851.26 fl=-1673.17 Vl=9.16 Ml=797.45 Pw=0.00 Mw=0.00
Frame2D_320: nodes ( Node_212 Node_213 )
material: ElasticSection
internal forces: f0=-844.87 V0=17.25 M0=-1328.12 fl=-844.87 Vl=17.25 Ml=1778.43 Pw=0.00 Mw=0.00
Frame2D_321: nodes ( Node_214 Node_215 )
material: ElasticSection
internal forces: f0=-3339.42 V0=-7.47 M0=673.83 fl=-3339.42 Vl=-7.47 Ml=-668.39 Pw=0.00 Mw=0.00
Frame2D_322: nodes ( Node_215 Node_216 )
material: ElasticSection
internal forces: f0=-2503.35 V0=-12.97 M0=1196.02 fl=-2503.35 Vl=-12.97 Ml=-1140.41 Pw=0.00 Mw=0.00
Frame2D_323: nodes ( Node_216 Node_217 )
material: ElasticSection
internal forces: f0=-1673.17 V0=-9.16 M0=851.26 fl=-1673.17 Vl=-9.16 Ml=-797.45 Pw=0.00 Mw=0.00
Frame2D_324: nodes ( Node_217 Node_218 )
material: ElasticSection
internal forces: f0=-844.87 V0=-17.25 M0=1328.12 fl=-844.87 Vl=-17.25 Ml=-1778.43 Pw=0.00 Mw=0.00
Frame2D_325: nodes ( Node_219 Node_220 )
material: ElasticSection
internal forces: f0=-1412.58 V0=28.72 M0=-2190.63 fl=-1412.58 Vl=28.72 Ml=2981.99 Pw=0.00 Mw=0.00
Frame2D_326: nodes ( Node_220 Node_221 )
material: ElasticSection
internal forces: f0=-1060.65 V0=54.15 M0=-4967.18 fl=-1060.65 Vl=54.15 Ml=4777.61 Pw=0.00 Mw=0.00
Frame2D_327: nodes ( Node_221 Node_222 )
material: ElasticSection
internal forces: f0=-702.83 V0=48.56 M0=-4417.41 fl=-702.83 Vl=48.56 Ml=4323.51 Pw=0.00 Mw=0.00
Frame2D_328: nodes ( Node_222 Node_223 )
material: ElasticSection
internal forces: f0=-343.13 V0=63.72 M0=-5307.41 fl=-343.13 Vl=63.72 Ml=6160.35 Pw=0.00 Mw=0.00
Frame2D_329: nodes ( Node_205 Node_210 )
material: ElasticSection
internal forces: f0=25.43 V0=-44.07 M0=7890.83 fl=25.43 Vl=-44.07 Ml=-2686.63 Pw=-396.00 Mw=-15840.00
Frame2D_330: nodes ( Node_210 Node_215 )
material: ElasticSection
internal forces: f0=19.93 V0=0.00 M0=-822.22 fl=19.93 Vl=0.00 Ml=-822.22 Pw=-396.00 Mw=-15840.00
Frame2D_331: nodes ( Node_215 Node_220 )
material: ElasticSection
internal forces: f0=25.43 V0=44.07 M0=-2686.63 fl=25.43 Vl=44.07 Ml=7890.83 Pw=-396.00 Mw=-15840.00
Frame2D_332: nodes ( Node_206 Node_211 )
material: ElasticSection
internal forces: f0=-5.60 V0=-38.17 M0=6644.98 fl=-5.60 Vl=-38.17 Ml=-2516.78 Pw=-396.00 Mw=-15840.00
Frame2D_333: nodes ( Node_211 Node_216 )
material: ElasticSection
internal forces: f0=-1.79 V0=0.00 M0=-525.10 fl=-1.79 Vl=0.00 Ml=-525.10 Pw=-396.00 Mw=-15840.00
Frame2D_334: nodes ( Node_216 Node_221 )
material: ElasticSection
internal forces: f0=-5.60 V0=38.17 M0=-2516.78 fl=-5.60 Vl=38.17 Ml=6644.98 Pw=-396.00 Mw=-15840.00
Frame2D_335: nodes ( Node_207 Node_212 )
material: ElasticSection
internal forces: f0=15.17 V0=-36.30 M0=6209.08 fl=15.17 Vl=-36.30 Ml=-2503.48 Pw=-396.00 Mw=-15840.00
Frame2D_336: nodes ( Node_212 Node_217 )
material: ElasticSection
internal forces: f0=7.08 V0=0.00 M0=-377.91 fl=7.08 Vl=0.00 Ml=-377.91 Pw=-396.00 Mw=-15840.00
Frame2D_337: nodes ( Node_217 Node_222 )
material: ElasticSection
internal forces: f0=15.17 V0=36.30 M0=-2503.48 fl=15.17 Vl=36.30 Ml=6209.08 Pw=-396.00 Mw=-15840.00
Frame2D_338: nodes ( Node_208 Node_213 )
material: ElasticSection
internal forces: f0=-63.72 V0=-52.87 M0=9679.65 fl=-63.72 Vl=-52.87 Ml=-3007.97 Pw=-396.00 Mw=-15840.00
Frame2D_339: nodes ( Node_213 Node_218 )
material: ElasticSection
internal forces: f0=-46.47 V0=0.00 M0=-1229.55 fl=-46.47 Vl=0.00 Ml=-1229.55 Pw=-396.00 Mw=-15840.00
Frame2D_340: nodes ( Node_218 Node_223 )
material: ElasticSection
internal forces: f0=-63.72 V0=52.87 M0=-3007.97 fl=-63.72 Vl=52.87 Ml=9679.65 Pw=-396.00 Mw=-15840.00
Total running time of the script: (0 minutes 0.690 seconds)