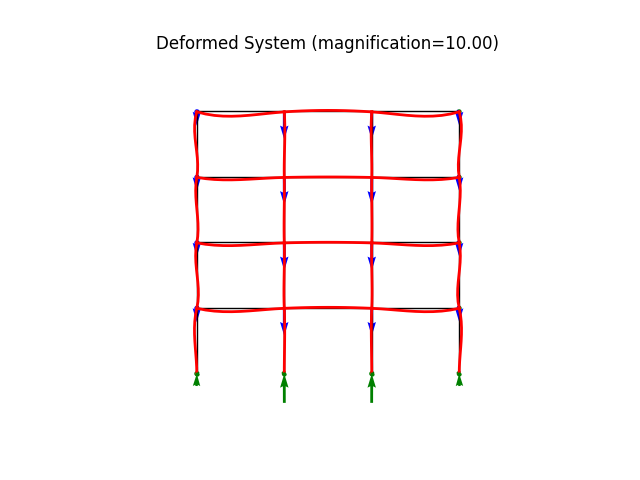
Frame with inclined support

modeled using * a linear 2D frame element * inclined boundary condition (using Transformation) * element loading

setting given parameters

N = 8	number of elements
L = 10.0 ft	segment length
MOE = 29000 ksi	modulus of elasticity
A = 1.04828 in^2	cross section area
I = 5.5908 in^4	moment of inertia
w = 0.333 * kip / ft	applied lateral load

Author: Peter Mackenzie-Helnwein

from random import betavariate

import numpy as np

from femedu.examples.Example import *

from femedu.domain import *
from femedu.solver import LinearSolver, NewtonRaphsonSolver
from femedu.elements.linear import Frame2D
from femedu.domain import Frame2dTransformation
from femedu.materials import ElasticSection


class ExampleFrame04(Example):


    def createMesh(self, nelem=4):
        """
        Creates a mesh using `nelem` elements for each of the straight segments.
        """
        if (not isinstance(nelem, int)) or nelem % 4:
            msg = "nelem must be an integer multiple of 4 (4,8,12,...)"
            raise TypeError(msg)

        # units
        inch = 1
        ft = 12 * inch
        kip = 1
        kips = kip
        lb = kip / 1000
        psi = lb / inch ** 2
        ksi = kip / inch ** 2
        degrees = np.pi / 180.

        # problem parameters
        MOE  =  29000 * ksi
        EI   = 162133 * kips * inch ** 2
        EA   =  30400 * kips
        L    =     10 * ft
        w0   =  0.333 * kip / ft
        beta = 30.0 * degrees  # slope of the upper support

        #
        # start meshing
        #
        s = np.linspace(0.0, 1.0, nelem // 2 + 1)

        params = dict(
            E = MOE,
            A = EA/MOE,
            I = EI/MOE,
        )

        material = ElasticSection(params)

        # nodes
        nodes  = [ Node(0.0, si * L) for si in s]
        nodes += [ Node(si * L * np.cos(np.radians(30.)), L + si * L * np.sin(np.radians(30.))) for si in s[1:]]

        # elements
        elements = [Frame2D(nodes[i], nodes[i+1], material) for i in range(nelem)]

        # fixities
        # ... the first node
        nodes[0].fixDOF(['ux','uy','rz'])
        # ... the last node
        nvec = [np.cos(beta), np.sin(beta)]            # vector parallel to the sliding plane of the upper support

        transform = Frame2dTransformation(nvec)        # an in-plane rotation
        nodes[-1].addTransformation(transform)         # defining a local frame for the last node

        nodes[-1].fixDOF(['uy', ])                     # fixing the LOCAL y-direction

        # load the top half of the vertical member
        # and the first half of the inclined member
        for i in range(nelem//4, 3*nelem//4):
            elements[i].setDistLoad(-w0)

        return (nodes, elements)

    def problem(self):
        # initialize a system model

        N  = 4     # number of elements

        # ========== setting global parameters ==============

        target_load_level = 1.

        # ========= build your structural model =============

        model = System()
        model.setSolver(NewtonRaphsonSolver())
        # model.setSolver(LinearSolver())

        nodes, elements = self.createMesh(N)

        model.addNode(*nodes)
        model.addElement(*elements)

        # show model information
        print(model)

        print("\n==== perform the analysis ===\n")

        # solve
        model.setLoadFactor(target_load_level)
        model.solve(verbose=True, max_steps=10)

        #
        # ==== create some nice plots ===
        #

        model.report()

        model.plot(factor=10.0, filename="frame4_deformed.png", show_bc=1)

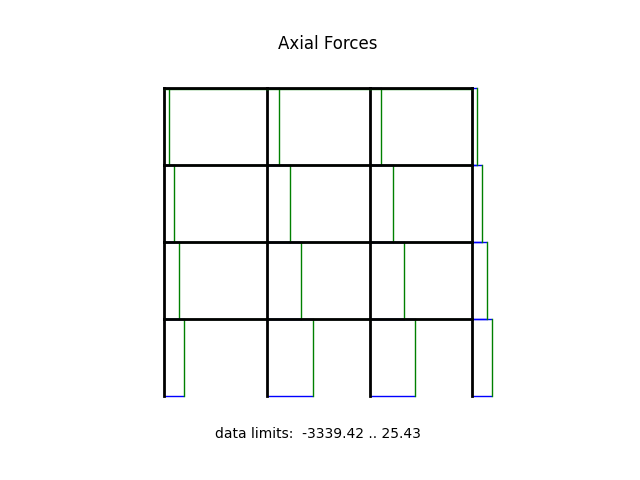
        model.beamValuePlot("F", filename="frame4_force.png")
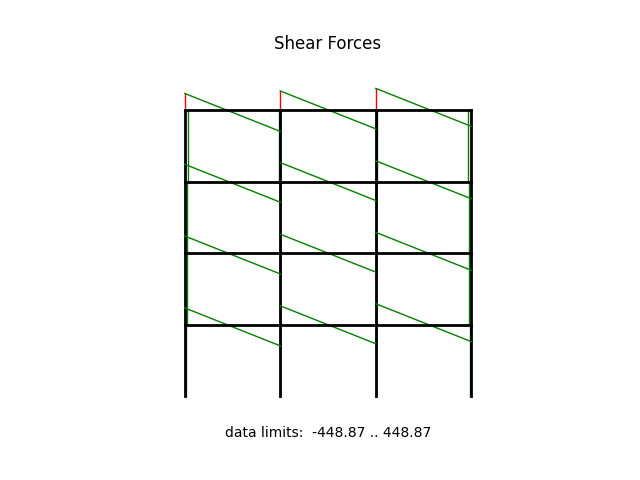
        model.beamValuePlot("V", filename="frame4_shear.png")
        model.beamValuePlot("M", filename="frame4_moment.png")

Run the example by creating an instance of the problem and executing it by calling Example.run()

if __name__ == "__main__":
    ex = ExampleFrame04()
    ex.run()

• 
• 
• 
• 

System object
Node_199(x=[0 0], u=None)
Node_200(x=[0 60], u=None)
Node_201(x=[0 120], u=None)
Node_202(x=[51.9615 150], u=None)
Node_203(x=[103.923 180], u=None)
Frame2D(Node_199, Node_200, ElasticSection(Material)({'E': 29000.0, 'A': 1.0482758620689656, 'I': 5.590793103448276, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_200, Node_201, ElasticSection(Material)({'E': 29000.0, 'A': 1.0482758620689656, 'I': 5.590793103448276, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_201, Node_202, ElasticSection(Material)({'E': 29000.0, 'A': 1.0482758620689656, 'I': 5.590793103448276, 'nu': 0.0, 'fy': 1e+30}))
Frame2D(Node_202, Node_203, ElasticSection(Material)({'E': 29000.0, 'A': 1.0482758620689656, 'I': 5.590793103448276, 'nu': 0.0, 'fy': 1e+30}))

==== perform the analysis ===

norm of the out-of-balance force:   1.1920e+01
norm of the out-of-balance force:   2.8602e-13
+

System Analysis Report
=======================

Nodes:
---------------------
  Node_199:
      x:    [0.000 0.000]
      fix:  ['ux', 'uy', 'rz']
      u:    [0.000 0.000 0.000]
  Node_200:
      x:    [0.000 60.000]
      u:    [1.001 -0.001 -0.026]
  Node_201:
      x:    [0.000 120.000]
      u:    [2.294 -0.002 -0.013]
  Node_202:
      x:    [51.962 150.000]
      u:    [2.296 -0.007 0.012]
  Node_203:
      x:    [103.923 180.000]
      local: x=[0.866 0.500], y=[-0.500 0.866]
      fix:  ['uy']
      u:    [1.719 0.993 0.023]

Elements:
---------------------
  Frame2D_309: nodes ( Node_199 Node_200 )
      material: ElasticSection
      internal forces: f0=-0.63 V0=2.03 M0=-130.69 fl=-0.63 Vl=2.03 Ml=-9.01 Pw=0.00 Mw=0.00
  Frame2D_310: nodes ( Node_200 Node_201 )
      material: ElasticSection
      internal forces: f0=-0.63 V0=1.20 M0=-0.69 fl=-0.63 Vl=1.20 Ml=71.05 Pw=-0.83 Mw=-8.33
  Frame2D_311: nodes ( Node_201 Node_202 )
      material: ElasticSection
      internal forces: f0=-0.00 V0=-0.11 M0=71.05 fl=-0.00 Vl=-0.11 Ml=64.66 Pw=-0.83 Mw=-8.33
  Frame2D_312: nodes ( Node_202 Node_203 )
      material: ElasticSection
      internal forces: f0=-0.00 V0=-0.94 M0=56.34 fl=-0.00 Vl=-0.94 Ml=0.00 Pw=0.00 Mw=0.00