Note
Go to the end to download the full example code
Patch test for triangular plate under in-plane loading
PatchMesher test for the LinearTriangle (Constant Strain Triangle)
import math
import numpy as np
from femedu.examples import Example
from femedu.domain import System, Node
from femedu.solver import NewtonRaphsonSolver
from femedu.elements.linear import Quad, Triangle
from femedu.materials import PlaneStress
from femedu.mesher import *
class ExamplePlate04(Example):
def problem(self):
# ========== setting mesh parameters ==============
Nx = 7 # number of elements in the mesh
Ny = 6 # number of elements in the mesh
Lx = 100.0 # length of plate in the x-direction
Ly = 80.0 # length of plate in the y-direction
# ========== setting material parameters ==============
params = dict(
E = 20000., # Young's modulus
nu = 0.250, # Poisson's ratio
t = 1.00 # thickness of the plate
)
# ========== setting load parameters ==============
px = 10.0 # uniform load normal to x=const
py = 0.0 # uniform load normal to y=const
pxy = 0.0 # uniform shear load on x=const and y=const
# ========== setting analysis parameters ==============
target_load_level = 1.00 # reference load
max_steps = 2 # number of load steps: 2 -> [0.0, 1.0]
# define a list of target load levels
load_levels = np.linspace(0, target_load_level, max_steps)
#
# ==== Build the system model ====
#
model = System()
model.setSolver(NewtonRaphsonSolver())
# create reference points
pt0 = (0,0)
pt1 = (0.5*Lx,0)
pt2 = (Lx,Ly)
pt3 = (0,Ly)
pt4 = (0.25*Lx, 0.0)
pt5 = (0.65*Lx, Ly/2)
pt6 = (0.55*Lx, Ly)
pt7 = (0.0, Ly/2)
pt8 = (0.325*Lx, 0.55*Ly)
pt9 = (Lx,0.0)
mesher1 = PatchMesher(model,
pt0, pt1, pt2, pt3, # corner nodes
pt4, pt5, pt6, pt7, # mid-side nodes
pt8) # center node
#nodes1, elements1 = mesher1.triangleMesh(Nx, Ny, LinearTriangle, PlaneStress(params))
nodes1, elements1 = mesher1.quadMesh(Nx, Ny, Quad, PlaneStress(params))
mesher2 = TriPatchMesher(model,
pt1, pt9, pt2, # corner nodes
None, None, pt5, # mid-side nodes
)
#mesher2.shift(1.25*Lx, Ly/2)
nodes2, elements2 = mesher2.triangleMesh(Ny, Triangle, PlaneStress(params))
#nodes2, elements2 = mesher2.quadMesh(Ny, Triangle, PlaneStress(params))
# tie the patches together
mesher1.tie(mesher2)
nodes = nodes1 + nodes2
elements = elements1 + elements2
# define support(s)
## find nodes at y==0 and x==0
for node in nodes:
X = node.getPos()
if math.isclose(X[0], 0.0):
node.fixDOF('ux') # horizontal support left side
if math.isclose(X[1], 0.0):
node.fixDOF('uy') # vertical support at y==0
# ==== complete the reference load ====
Xo = np.array([Lx, 0.0])
No = np.array([1.0, 0.0])
for node in nodes:
X = node.getPos()
if math.isclose(X[0],Lx):
print(node)
for elem in node.elements:
print('+', elem)
for face in elem.faces:
for x, area in zip(face.pos, face.area):
if np.abs( (x - Xo) @ No ) < 1.0e-2 and No @ area / np.linalg.norm(area):
face.setLoad(px, 0.0)
#model.report()
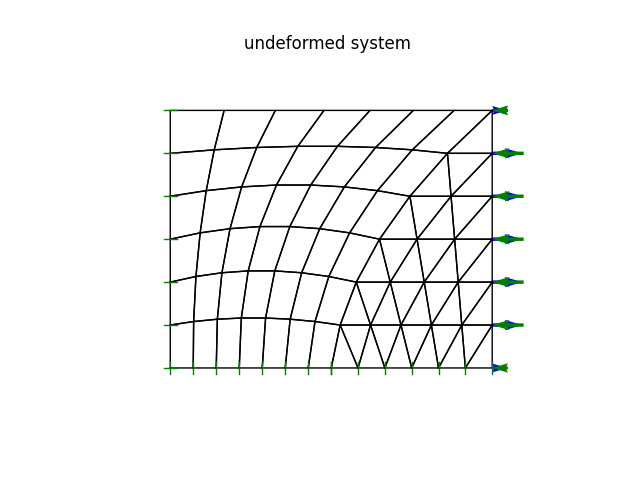
model.plot(factor=0, title="undeformed system", filename="plate04_undeformed.png", show_bc=1, show_loads=1)
model.setLoadFactor(10.0)
model.solve()
#model.report()
model.plot(factor=10., filename="plate04_deformed.png")
Run the example by creating an instance of the problem and executing it by calling Example.run()
if __name__ == "__main__":
ex = ExamplePlate04()
ex.run()
Node_721:
x: [100. 80.]
u: None
+ Quad_986: nodes ( Node_712 Node_713 Node_721 Node_720 )
material: list
strain (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
strain (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
strain (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
strain (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_1021: nodes ( Node_747 Node_748 Node_749 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
Node_728:
x: [100. 0.]
fix: ['uy']
u: None
+ Triangle_992: nodes ( Node_727 Node_728 Node_734 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
Node_734:
x: [100. 13.33333333]
u: None
+ Triangle_992: nodes ( Node_727 Node_728 Node_734 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_1001: nodes ( Node_733 Node_734 Node_739 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_1002: nodes ( Node_734 Node_733 Node_727 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
Node_739:
x: [100. 26.66666667]
u: None
+ Triangle_1001: nodes ( Node_733 Node_734 Node_739 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_1009: nodes ( Node_738 Node_739 Node_743 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_1010: nodes ( Node_739 Node_738 Node_733 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
Node_743:
x: [100. 40.]
u: None
+ Triangle_1009: nodes ( Node_738 Node_739 Node_743 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_1015: nodes ( Node_742 Node_743 Node_746 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_1016: nodes ( Node_743 Node_742 Node_738 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
Node_746:
x: [100. 53.33333333]
u: None
+ Triangle_1015: nodes ( Node_742 Node_743 Node_746 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_1019: nodes ( Node_745 Node_746 Node_748 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_1020: nodes ( Node_746 Node_745 Node_742 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
Node_748:
x: [100. 66.66666667]
u: None
+ Triangle_1019: nodes ( Node_745 Node_746 Node_748 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_1021: nodes ( Node_747 Node_748 Node_749 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_1022: nodes ( Node_748 Node_747 Node_745 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
Node_749:
x: [100. 80.]
following Node_721
u: None
+ Triangle_1021: nodes ( Node_747 Node_748 Node_749 )
material: PlaneStress
strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+
Total running time of the script: (0 minutes 0.865 seconds)