Note
Go to the end to download the full example code
Patch test for quadrilateral plate elements under in-plane loading
The patch test is an empirical minimum test which every finite element has to pass to ensure convergence with mesh refinement.
It consists of a problem for which a known homogeneous solution exists. For plates, we commonly use a rectangular plate subject to homogeneous edge loading, e.g., constant tension in the x-direction, or constant shear, etc.
The mesh must contain distorted elements and at least one element not attached to any node on the boundary.
Author: Peter Mackenzie-Helnwein
import numpy as np
from femedu.examples import Example
from femedu.domain import System, Node
from femedu.solver import NewtonRaphsonSolver
from femedu.elements.linear import Quad
from femedu.materials import PlaneStress
class ExamplePlate09(Example):
def problem(self):
# ========== setting mesh parameters ==============
N = 8 # number of elements in the mesh
Lx = 100.0 # length of plate in the x-direction
Ly = 80.0 # length of plate in the y-direction
# ========== setting material parameters ==============
params = dict(
E = 20000., # Young's modulus
nu = 0.250, # Poisson's ratio
t = 1.00 # thickness of the plate
)
# ========== setting load parameters ==============
px = 10.0 # uniform load normal to x=const
py = 0.0 # uniform load normal to y=const
pxy = 0.0 # uniform shear load on x=const and y=const
# ========== setting analysis parameters ==============
target_load_level = 1.00 # reference load
max_steps = 2 # number of load steps: 2 -> [0.0, 1.0]
# define a list of target load levels
load_levels = np.linspace(0, target_load_level, max_steps)
#
# ==== Build the system model ====
#
model = System()
model.setSolver(NewtonRaphsonSolver())
# create nodes
nodes = (
Node(0.0*Lx, 0.0*Ly), # nd 0
Node(0.2*Lx, 0.0*Ly), # nd 1
Node(0.5*Lx, 0.0*Ly), # nd 2
Node(0.7*Lx, 0.0*Ly), # nd 3
Node(1.0*Lx, 0.0*Ly), # nd 4
#
Node(0.0*Lx, 0.2*Ly), # nd 5
Node(0.15*Lx,0.3*Ly), # nd 6
Node(0.5*Lx, 0.2*Ly), # nd 7
Node(0.8*Lx, 0.3*Ly), # nd 8
Node(1.0*Lx, 0.2*Ly), # nd 9
#
Node(0.0*Lx, 0.6*Ly), # nd 10
Node(0.2*Lx, 0.5*Ly), # nd 11
Node(0.7*Lx, 0.7*Ly), # nd 12
Node(0.9*Lx, 0.6*Ly), # nd 13
Node(1.0*Lx, 0.7*Ly), # nd 14
#
Node(0.0*Lx, 1.0*Ly), # nd 15
Node(0.3*Lx, 1.0*Ly), # nd 16
Node(0.55*Lx,1.0*Ly), # nd 17
Node(0.8*Lx, 1.0*Ly), # nd 18
Node(1.0*Lx, 1.0*Ly), # nd 19
)
elements = (
Quad(nodes[0],nodes[1],nodes[6],nodes[5],PlaneStress(params)), # elem 0
Quad(nodes[1],nodes[2],nodes[7],nodes[6],PlaneStress(params)), # elem 1
Quad(nodes[2],nodes[3],nodes[8],nodes[7],PlaneStress(params)), # elem 2
Quad(nodes[3],nodes[4],nodes[9],nodes[8],PlaneStress(params)), # elem 3
#
Quad(nodes[5],nodes[6],nodes[11],nodes[10],PlaneStress(params)), # elem 4
Quad(nodes[6],nodes[7],nodes[12],nodes[11],PlaneStress(params)), # elem 5
Quad(nodes[7],nodes[8],nodes[13],nodes[12],PlaneStress(params)), # elem 6
Quad(nodes[8],nodes[9],nodes[14],nodes[13],PlaneStress(params)), # elem 7
#
Quad(nodes[10],nodes[11],nodes[16],nodes[15],PlaneStress(params)), # elem 8
Quad(nodes[11],nodes[12],nodes[17],nodes[16],PlaneStress(params)), # elem 9
Quad(nodes[12],nodes[13],nodes[18],nodes[17],PlaneStress(params)), # elem 10
Quad(nodes[13],nodes[14],nodes[19],nodes[18],PlaneStress(params)), # elem 11
#
)
model.addNode(*nodes)
model.addElement(*elements)
# define support(s)
fix_x = (0,)
fix_y = (0,4)
for idx in fix_x:
nodes[idx].fixDOF('ux') # horizontal support left end
for idx in fix_y:
nodes[idx].fixDOF('uy') # vertical support right end
# ==== complete the reference load ====
# surface loads on the left side
elements[0].setSurfaceLoad(3,px)
elements[4].setSurfaceLoad(3,px)
elements[8].setSurfaceLoad(3,px)
# surface loads on the right side
elements[ 3].setSurfaceLoad(1,px)
elements[ 7].setSurfaceLoad(1,px)
elements[11].setSurfaceLoad(1,px)
# these are only nodal forces as part of the reference load
# .. load only the upper node
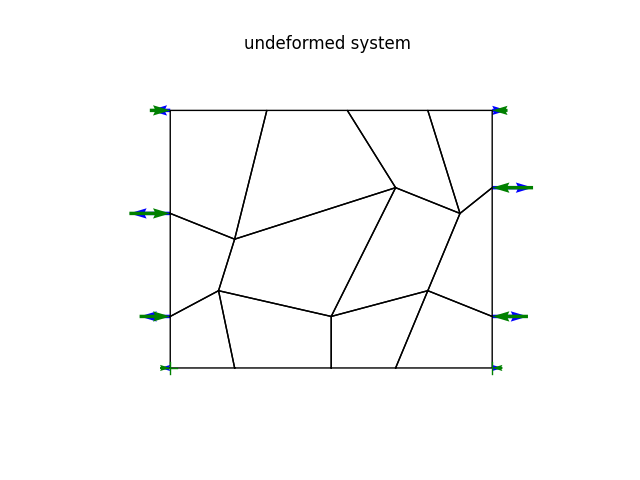
model.plot(factor=0., title="undeformed system", filename="plate09_undeformed.png", show_bc=1)
model.setLoadFactor(0.0)
model.solve()
# for k in range(25):
# name = f"plate08_mode{k:2d}.png"
# model.plotBucklingMode(mode=k,filename=name,factor=25)
model.setLoadFactor(10.0)
model.solve()
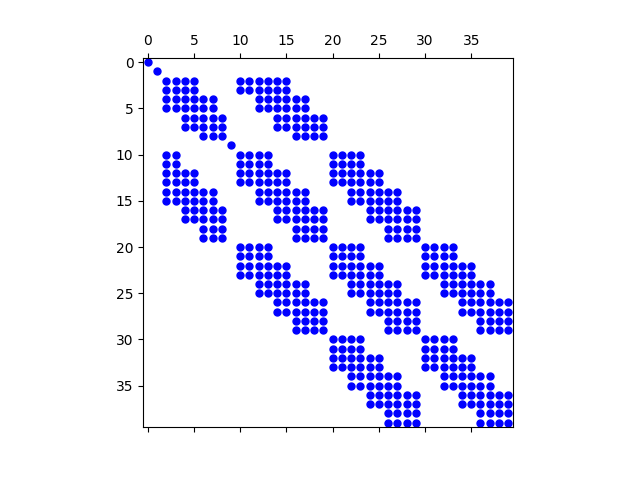
model.solver.showKt(filename="plate09_spy_Kt.png")
model.report()
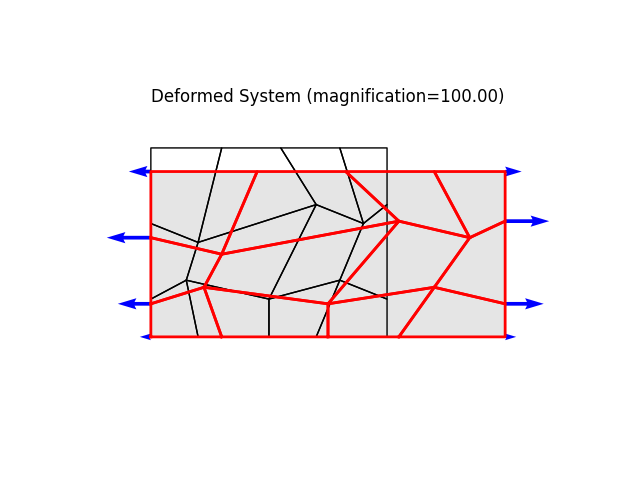
model.plot(factor=100., filename="plate09_deformed.png")
Run the example by creating an instance of the problem and executing it by calling Example.run()
if __name__ == "__main__":
ex = ExamplePlate09()
ex.run()
+
+
System Analysis Report
=======================
Nodes:
---------------------
Node_1398:
x: [0. 0.]
fix: ['ux', 'uy']
u: [0. 0.]
Node_1399:
x: [20. 0.]
u: [ 1.00000000e-01 -2.47751692e-15]
Node_1400:
x: [50. 0.]
u: [ 2.50000000e-01 -3.49489281e-15]
Node_1401:
x: [70. 0.]
u: [ 3.50000000e-01 -7.09305773e-15]
Node_1402:
x: [100. 0.]
fix: ['uy']
u: [0.5 0. ]
Node_1403:
x: [ 0. 16.]
u: [-2.77140442e-16 -2.00000000e-02]
Node_1404:
x: [15. 24.]
u: [ 0.075 -0.03 ]
Node_1405:
x: [50. 16.]
u: [ 0.25 -0.02]
Node_1406:
x: [80. 24.]
u: [ 0.4 -0.03]
Node_1407:
x: [100. 16.]
u: [ 0.5 -0.02]
Node_1408:
x: [ 0. 48.]
u: [ 4.82755937e-15 -6.00000000e-02]
Node_1409:
x: [20. 40.]
u: [ 0.1 -0.05]
Node_1410:
x: [70. 56.]
u: [ 0.35 -0.07]
Node_1411:
x: [90. 48.]
u: [ 0.45 -0.06]
Node_1412:
x: [100. 56.]
u: [ 0.5 -0.07]
Node_1413:
x: [ 0. 80.]
u: [ 7.45807055e-15 -1.00000000e-01]
Node_1414:
x: [30. 80.]
u: [ 0.15 -0.1 ]
Node_1415:
x: [55. 80.]
u: [ 0.275 -0.1 ]
Node_1416:
x: [80. 80.]
u: [ 0.4 -0.1]
Node_1417:
x: [100. 80.]
u: [ 0.5 -0.1]
Elements:
---------------------
Quad_1806: nodes ( Node_1398 Node_1399 Node_1404 Node_1403 )
material: list
strain (0): xx=5.000e-03 yy=-1.250e-03 xy=-1.104e-16 zz=-9.375e-04
stress (0): xx=1.000e+02 yy=2.366e-12 xy=-8.833e-13 zz=0.000e+00
strain (1): xx=5.000e-03 yy=-1.250e-03 xy=1.272e-17 zz=-9.375e-04
stress (1): xx=1.000e+02 yy=-1.183e-12 xy=1.018e-13 zz=0.000e+00
strain (2): xx=5.000e-03 yy=-1.250e-03 xy=-1.749e-16 zz=-9.375e-04
stress (2): xx=1.000e+02 yy=2.366e-12 xy=-1.399e-12 zz=0.000e+00
strain (3): xx=5.000e-03 yy=-1.250e-03 xy=1.008e-16 zz=-9.375e-04
stress (3): xx=1.000e+02 yy=0.000e+00 xy=8.065e-13 zz=0.000e+00
Quad_1807: nodes ( Node_1399 Node_1400 Node_1405 Node_1404 )
material: list
strain (0): xx=5.000e-03 yy=-1.250e-03 xy=7.529e-17 zz=-9.375e-04
stress (0): xx=1.000e+02 yy=2.370e-12 xy=6.023e-13 zz=0.000e+00
strain (1): xx=5.000e-03 yy=-1.250e-03 xy=-1.356e-16 zz=-9.375e-04
stress (1): xx=1.000e+02 yy=1.187e-12 xy=-1.085e-12 zz=0.000e+00
strain (2): xx=5.000e-03 yy=-1.250e-03 xy=2.377e-17 zz=-9.375e-04
stress (2): xx=1.000e+02 yy=-3.553e-12 xy=1.901e-13 zz=0.000e+00
strain (3): xx=5.000e-03 yy=-1.250e-03 xy=3.897e-17 zz=-9.375e-04
stress (3): xx=1.000e+02 yy=1.187e-12 xy=3.118e-13 zz=0.000e+00
Quad_1808: nodes ( Node_1400 Node_1401 Node_1406 Node_1405 )
material: list
strain (0): xx=5.000e-03 yy=-1.250e-03 xy=3.344e-16 zz=-9.375e-04
stress (0): xx=1.000e+02 yy=0.000e+00 xy=2.675e-12 zz=0.000e+00
strain (1): xx=5.000e-03 yy=-1.250e-03 xy=2.241e-16 zz=-9.375e-04
stress (1): xx=1.000e+02 yy=2.370e-12 xy=1.793e-12 zz=0.000e+00
strain (2): xx=5.000e-03 yy=-1.250e-03 xy=4.129e-16 zz=-9.375e-04
stress (2): xx=1.000e+02 yy=-1.183e-12 xy=3.304e-12 zz=0.000e+00
strain (3): xx=5.000e-03 yy=-1.250e-03 xy=-7.355e-17 zz=-9.375e-04
stress (3): xx=1.000e+02 yy=3.553e-12 xy=-5.884e-13 zz=0.000e+00
Quad_1809: nodes ( Node_1401 Node_1402 Node_1407 Node_1406 )
material: list
strain (0): xx=5.000e-03 yy=-1.250e-03 xy=-3.343e-16 zz=-9.375e-04
stress (0): xx=1.000e+02 yy=-5.922e-12 xy=-2.674e-12 zz=0.000e+00
strain (1): xx=5.000e-03 yy=-1.250e-03 xy=-1.446e-16 zz=-9.375e-04
stress (1): xx=1.000e+02 yy=-2.370e-12 xy=-1.157e-12 zz=0.000e+00
strain (2): xx=5.000e-03 yy=-1.250e-03 xy=9.823e-17 zz=-9.375e-04
stress (2): xx=1.000e+02 yy=0.000e+00 xy=7.859e-13 zz=0.000e+00
strain (3): xx=5.000e-03 yy=-1.250e-03 xy=2.679e-16 zz=-9.375e-04
stress (3): xx=1.000e+02 yy=2.366e-12 xy=2.143e-12 zz=0.000e+00
Quad_1810: nodes ( Node_1403 Node_1404 Node_1409 Node_1408 )
material: list
strain (0): xx=5.000e-03 yy=-1.250e-03 xy=5.662e-18 zz=-9.375e-04
stress (0): xx=1.000e+02 yy=2.366e-12 xy=4.530e-14 zz=0.000e+00
strain (1): xx=5.000e-03 yy=-1.250e-03 xy=-4.978e-17 zz=-9.375e-04
stress (1): xx=1.000e+02 yy=5.922e-12 xy=-3.983e-13 zz=0.000e+00
strain (2): xx=5.000e-03 yy=-1.250e-03 xy=-7.141e-18 zz=-9.375e-04
stress (2): xx=1.000e+02 yy=1.187e-12 xy=-5.713e-14 zz=0.000e+00
strain (3): xx=5.000e-03 yy=-1.250e-03 xy=-1.342e-16 zz=-9.375e-04
stress (3): xx=1.000e+02 yy=8.292e-12 xy=-1.074e-12 zz=0.000e+00
Quad_1811: nodes ( Node_1404 Node_1405 Node_1410 Node_1409 )
material: list
strain (0): xx=5.000e-03 yy=-1.250e-03 xy=1.100e-16 zz=-9.375e-04
stress (0): xx=1.000e+02 yy=2.366e-12 xy=8.800e-13 zz=0.000e+00
strain (1): xx=5.000e-03 yy=-1.250e-03 xy=-3.472e-16 zz=-9.375e-04
stress (1): xx=1.000e+02 yy=-1.183e-12 xy=-2.777e-12 zz=0.000e+00
strain (2): xx=5.000e-03 yy=-1.250e-03 xy=1.983e-16 zz=-9.375e-04
stress (2): xx=1.000e+02 yy=-2.370e-12 xy=1.586e-12 zz=0.000e+00
strain (3): xx=5.000e-03 yy=-1.250e-03 xy=-2.046e-16 zz=-9.375e-04
stress (3): xx=1.000e+02 yy=3.553e-12 xy=-1.637e-12 zz=0.000e+00
Quad_1812: nodes ( Node_1405 Node_1406 Node_1411 Node_1410 )
material: list
strain (0): xx=5.000e-03 yy=-1.250e-03 xy=8.123e-17 zz=-9.375e-04
stress (0): xx=1.000e+02 yy=3.553e-12 xy=6.498e-13 zz=0.000e+00
strain (1): xx=5.000e-03 yy=-1.250e-03 xy=-3.826e-17 zz=-9.375e-04
stress (1): xx=1.000e+02 yy=2.370e-12 xy=-3.061e-13 zz=0.000e+00
strain (2): xx=5.000e-03 yy=-1.250e-03 xy=-3.527e-16 zz=-9.375e-04
stress (2): xx=1.000e+02 yy=-2.370e-12 xy=-2.821e-12 zz=0.000e+00
strain (3): xx=5.000e-03 yy=-1.250e-03 xy=1.849e-16 zz=-9.375e-04
stress (3): xx=1.000e+02 yy=7.105e-12 xy=1.479e-12 zz=0.000e+00
Quad_1813: nodes ( Node_1406 Node_1407 Node_1412 Node_1411 )
material: list
strain (0): xx=5.000e-03 yy=-1.250e-03 xy=-7.082e-17 zz=-9.375e-04
stress (0): xx=1.000e+02 yy=-1.183e-12 xy=-5.666e-13 zz=0.000e+00
strain (1): xx=5.000e-03 yy=-1.250e-03 xy=-2.260e-16 zz=-9.375e-04
stress (1): xx=1.000e+02 yy=-2.370e-12 xy=-1.808e-12 zz=0.000e+00
strain (2): xx=5.000e-03 yy=-1.250e-03 xy=-9.509e-16 zz=-9.375e-04
stress (2): xx=1.000e+02 yy=-1.303e-11 xy=-7.607e-12 zz=0.000e+00
strain (3): xx=5.000e-03 yy=-1.250e-03 xy=4.363e-16 zz=-9.375e-04
stress (3): xx=1.000e+02 yy=-3.553e-12 xy=3.490e-12 zz=0.000e+00
Quad_1814: nodes ( Node_1408 Node_1409 Node_1414 Node_1413 )
material: list
strain (0): xx=5.000e-03 yy=-1.250e-03 xy=-9.357e-18 zz=-9.375e-04
stress (0): xx=1.000e+02 yy=5.922e-12 xy=-7.486e-14 zz=0.000e+00
strain (1): xx=5.000e-03 yy=-1.250e-03 xy=7.244e-17 zz=-9.375e-04
stress (1): xx=1.000e+02 yy=3.553e-12 xy=5.795e-13 zz=0.000e+00
strain (2): xx=5.000e-03 yy=-1.250e-03 xy=1.508e-16 zz=-9.375e-04
stress (2): xx=1.000e+02 yy=3.553e-12 xy=1.206e-12 zz=0.000e+00
strain (3): xx=5.000e-03 yy=-1.250e-03 xy=4.473e-17 zz=-9.375e-04
stress (3): xx=1.000e+02 yy=0.000e+00 xy=3.578e-13 zz=0.000e+00
Quad_1815: nodes ( Node_1409 Node_1410 Node_1415 Node_1414 )
material: list
strain (0): xx=5.000e-03 yy=-1.250e-03 xy=1.955e-17 zz=-9.375e-04
stress (0): xx=1.000e+02 yy=-4.736e-12 xy=1.564e-13 zz=0.000e+00
strain (1): xx=5.000e-03 yy=-1.250e-03 xy=1.000e-16 zz=-9.375e-04
stress (1): xx=1.000e+02 yy=-8.288e-12 xy=8.001e-13 zz=0.000e+00
strain (2): xx=5.000e-03 yy=-1.250e-03 xy=-3.603e-16 zz=-9.375e-04
stress (2): xx=1.000e+02 yy=3.553e-12 xy=-2.883e-12 zz=0.000e+00
strain (3): xx=5.000e-03 yy=-1.250e-03 xy=-3.240e-16 zz=-9.375e-04
stress (3): xx=1.000e+02 yy=-4.739e-12 xy=-2.592e-12 zz=0.000e+00
Quad_1816: nodes ( Node_1410 Node_1411 Node_1416 Node_1415 )
material: list
strain (0): xx=5.000e-03 yy=-1.250e-03 xy=1.873e-16 zz=-9.375e-04
stress (0): xx=1.000e+02 yy=-3.553e-12 xy=1.498e-12 zz=0.000e+00
strain (1): xx=5.000e-03 yy=-1.250e-03 xy=-2.483e-17 zz=-9.375e-04
stress (1): xx=1.000e+02 yy=3.553e-12 xy=-1.986e-13 zz=0.000e+00
strain (2): xx=5.000e-03 yy=-1.250e-03 xy=2.034e-17 zz=-9.375e-04
stress (2): xx=1.000e+02 yy=-2.366e-12 xy=1.627e-13 zz=0.000e+00
strain (3): xx=5.000e-03 yy=-1.250e-03 xy=2.146e-16 zz=-9.375e-04
stress (3): xx=1.000e+02 yy=9.472e-12 xy=1.717e-12 zz=0.000e+00
Quad_1817: nodes ( Node_1411 Node_1412 Node_1417 Node_1416 )
material: list
strain (0): xx=5.000e-03 yy=-1.250e-03 xy=-1.364e-16 zz=-9.375e-04
stress (0): xx=1.000e+02 yy=1.183e-12 xy=-1.091e-12 zz=0.000e+00
strain (1): xx=5.000e-03 yy=-1.250e-03 xy=-1.167e-16 zz=-9.375e-04
stress (1): xx=1.000e+02 yy=4.739e-12 xy=-9.338e-13 zz=0.000e+00
strain (2): xx=5.000e-03 yy=-1.250e-03 xy=2.250e-16 zz=-9.375e-04
stress (2): xx=1.000e+02 yy=9.475e-12 xy=1.800e-12 zz=0.000e+00
strain (3): xx=5.000e-03 yy=-1.250e-03 xy=7.021e-17 zz=-9.375e-04
stress (3): xx=1.000e+02 yy=1.183e-12 xy=5.617e-13 zz=0.000e+00
/usr/local/lib/python3.11/site-packages/matplotlib/quiver.py:632: RuntimeWarning: Mean of empty slice.
amean = a.mean()
/usr/local/lib/python3.11/site-packages/numpy/core/_methods.py:129: RuntimeWarning: invalid value encountered in scalar divide
ret = ret.dtype.type(ret / rcount)
Total running time of the script: (0 minutes 0.549 seconds)