Simple triangular truss.

The system is statically determined and allows for easy validation of calculated deformation, reactions and internal forces.

Author: Peter Mackenzie-Helnwein

Setup

from femedu.examples import Example

from femedu.domain import System, Node
from femedu.elements.linear import Truss
from femedu.materials import FiberMaterial

Create the example by subclassing the Example

class ExampleTruss01(Example):

    def problem(self):
        # initialize a system model
        B = 6.0 * 12
        H = 3.0 * 12
        params = {'E': 10., 'A': 1., 'nu': 0.0, 'fy': 1.e30}

        model = System()

        # create nodes
        nd0 = Node(0.0, 0.0)
        nd1 = Node(  B, 0.0)
        nd2 = Node(0.5*B, H)

        model.addNode(nd0, nd1, nd2)

        # create elements
        model.addElement(Truss(nd0, nd1, FiberMaterial(params)))  # bottom 1
        model.addElement(Truss(nd0, nd2, FiberMaterial(params)))  # up right diag 1
        model.addElement(Truss(nd1, nd2, FiberMaterial(params)))  # up left diag 1

        # define support(s)
        nd0.fixDOF('ux', 'uy')    # pin support left end
        nd1.fixDOF('uy')            # roller support right end

        # add loads
        # .. load only the upper nodes
        nd2.setLoad([0.0, -1.0], ('ux', 'uy'))

        # analyze the model
        model.solve()

        # write out report
        model.report()

        # create plots
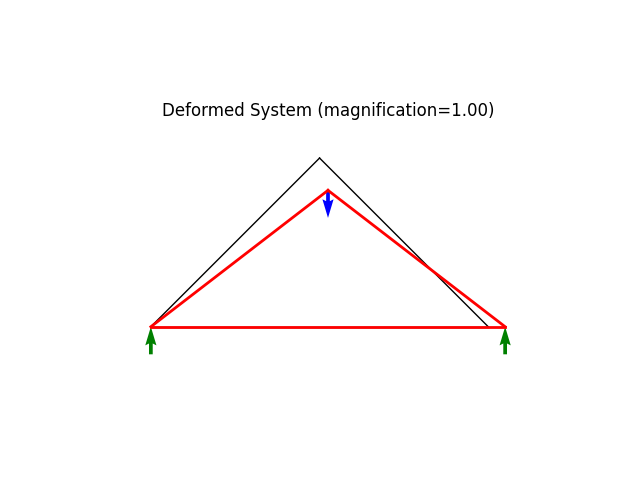
        model.plot(factor=1., filename="truss01_deformed.png")
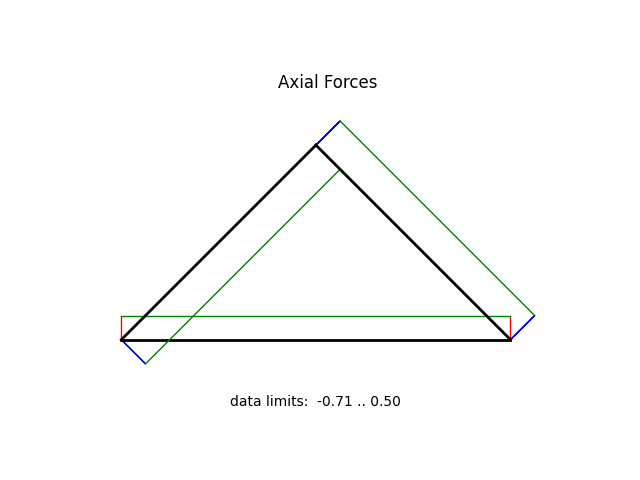
        model.beamValuePlot('f',filename="truss01_forces.png")

Run the example by creating an instance of the problem and executing it by calling Example.run()

if __name__ == "__main__":
    ex = ExampleTruss01()
    ex.run()

• 
• 

System Analysis Report
=======================

Nodes:
---------------------
  Node_24:
      x:    [0. 0.]
      fix:  ['ux', 'uy']
      u:    [0. 0.]
  Node_25:
      x:    [72.  0.]
      fix:  ['uy']
      u:    [3.6 0. ]
  Node_26:
      x:    [36. 36.]
      P:    [ 0. -1.]
      u:    [ 1.8        -6.89116882]

Elements:
---------------------
  Truss: Node_24 to Node_25:
      material properties: FiberMaterial(Material)({'E': 10.0, 'A': 1.0, 'nu': 0.0, 'fy': 1e+30})  strain:0.04999999999999999   stress:{'xx': 0.4999999999999999, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
      internal force: 0.4999999999999999
  Truss: Node_24 to Node_26:
      material properties: FiberMaterial(Material)({'E': 10.0, 'A': 1.0, 'nu': 0.0, 'fy': 1e+30})  strain:-0.07071067811865474   stress:{'xx': -0.7071067811865474, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
      internal force: -0.7071067811865474
  Truss: Node_25 to Node_26:
      material properties: FiberMaterial(Material)({'E': 10.0, 'A': 1.0, 'nu': 0.0, 'fy': 1e+30})  strain:-0.07071067811865472   stress:{'xx': -0.7071067811865472, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
      internal force: -0.7071067811865472