Note
Go to the end to download the full example code
Statically determinate truss bridge.
The system is statically determined and allows for relatively easy validation of calculated deformation, reactions and internal forces.
Author: Peter Mackenzie-Helnwein
from femedu.examples import Example
from femedu.domain import System, Node
from femedu.solver import NewtonRaphsonSolver
from femedu.elements.linear import Truss
from femedu.materials import FiberMaterial
class ExampleTruss02(Example):
def problem(self):
# initialize a system model
P = -10.0 # reference load on top nodes
B = 6.0 * 12 # with of one bay in inches
H = 8.0 * 12 # height of one bay in inches
# material model parameters
params = {'E': 10000., 'A': 3., 'nu': 0.0, 'fy': 1.e30}
model = System()
model.setSolver(NewtonRaphsonSolver())
# create nodes
nd0 = Node(0.0, 0.0)
nd1 = Node( B, 0.0)
nd2 = Node(2*B, 0.0)
nd3 = Node(3*B, 0.0)
nd4 = Node(4*B, 0.0)
nd5 = Node(0.5*B, H)
nd6 = Node(1.5*B, H)
nd7 = Node(2.5*B, H)
nd8 = Node(3.5*B, H)
model.addNode(nd0, nd1, nd2, nd3, nd4, nd5, nd6, nd7, nd8)
# create elements
model.addElement(Truss(nd0, nd1, FiberMaterial(params))) # bottom 1
model.addElement(Truss(nd1, nd2, FiberMaterial(params))) # bottom 2
model.addElement(Truss(nd2, nd3, FiberMaterial(params))) # bottom 3
model.addElement(Truss(nd3, nd4, FiberMaterial(params))) # bottom 4
model.addElement(Truss(nd5, nd6, FiberMaterial(params))) # upper 1
model.addElement(Truss(nd6, nd7, FiberMaterial(params))) # upper 2
model.addElement(Truss(nd7, nd8, FiberMaterial(params))) # upper 3
model.addElement(Truss(nd0, nd5, FiberMaterial(params))) # up right diag 1
model.addElement(Truss(nd1, nd6, FiberMaterial(params))) # up right diag 2
model.addElement(Truss(nd2, nd7, FiberMaterial(params))) # up right diag 3
model.addElement(Truss(nd3, nd8, FiberMaterial(params))) # up right diag 4
model.addElement(Truss(nd1, nd5, FiberMaterial(params))) # up left diag 1
model.addElement(Truss(nd2, nd6, FiberMaterial(params))) # up left diag 2
model.addElement(Truss(nd3, nd7, FiberMaterial(params))) # up left diag 3
model.addElement(Truss(nd4, nd8, FiberMaterial(params))) # up left diag 4
# define support(s)
nd0.fixDOF('ux', 'uy') # horizontal support left end
nd4.fixDOF('uy') # vertical support right end
# add loads
# .. load only the upper nodes
nd5.setLoad((P,), ('uy',))
nd6.setLoad((P,), ('uy',))
nd7.setLoad((P,), ('uy',))
nd8.setLoad((P,), ('uy',))
model.setLoadFactor(0.0)
model.plot(factor=1., filename="truss02_undeformed.png", title="Undeformed System", show_bc=1)
# analyze the model
model.setLoadFactor(1.0)
model.solve()
# write out report
model.report()
# create plots
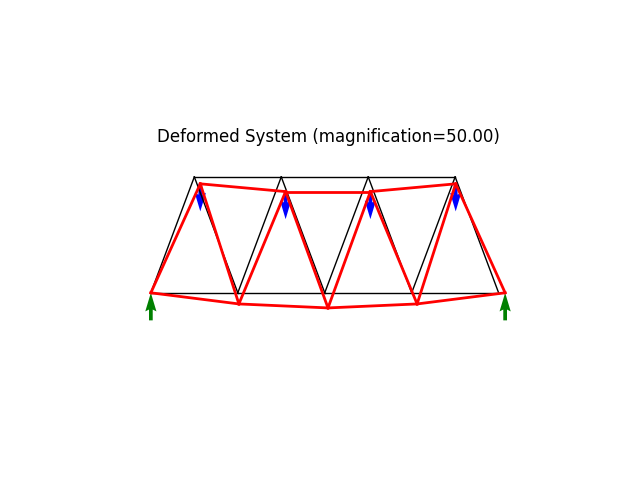
model.plot(factor=50., filename="truss02_deformed.png", show_loads=1, show_reactions=1)
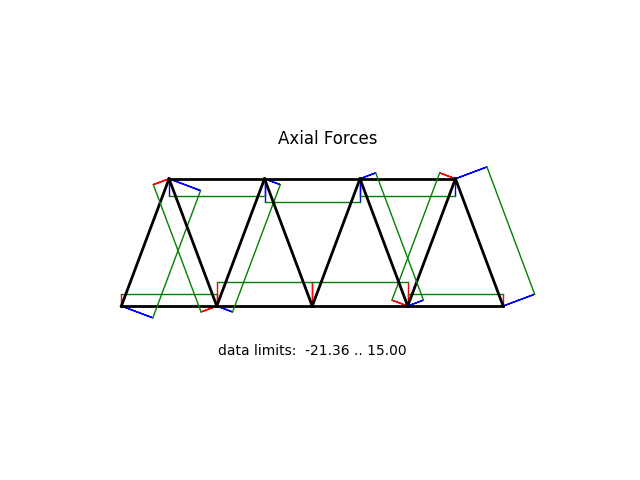
model.beamValuePlot('f',filename="truss02_forces.png")
Run the example by creating an instance of the problem and executing it by calling Example.run()
if __name__ == "__main__":
ex = ExampleTruss02()
ex.run()
/usr/local/lib/python3.11/site-packages/matplotlib/quiver.py:632: RuntimeWarning: Mean of empty slice.
amean = a.mean()
/usr/local/lib/python3.11/site-packages/numpy/core/_methods.py:129: RuntimeWarning: invalid value encountered in scalar divide
ret = ret.dtype.type(ret / rcount)
+
System Analysis Report
=======================
Nodes:
---------------------
Node_27:
x: [0. 0.]
fix: ['ux', 'uy']
u: [0. 0.]
Node_28:
x: [72. 0.]
u: [ 0.018 -0.18444605]
Node_29:
x: [144. 0.]
u: [ 0.054 -0.25042807]
Node_30:
x: [216. 0.]
u: [ 0.09 -0.18444605]
Node_31:
x: [288. 0.]
fix: ['uy']
u: [0.108 0. ]
Node_32:
x: [36. 96.]
P: [ 0. -10.]
u: [ 0.099 -0.11508903]
Node_33:
x: [108. 96.]
P: [ 0. -10.]
u: [ 0.072 -0.24367807]
Node_34:
x: [180. 96.]
P: [ 0. -10.]
u: [ 0.036 -0.24367807]
Node_35:
x: [252. 96.]
P: [ 0. -10.]
u: [ 0.009 -0.11508903]
Elements:
---------------------
Truss: Node_27 to Node_28:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:0.00025000000000000017 stress:{'xx': 2.5000000000000018, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: 7.500000000000005
Truss: Node_28 to Node_29:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:0.0005 stress:{'xx': 5.0, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: 15.0
Truss: Node_29 to Node_30:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:0.0005000000000000002 stress:{'xx': 5.000000000000003, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: 15.000000000000007
Truss: Node_30 to Node_31:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:0.00025 stress:{'xx': 2.5, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: 7.5
Truss: Node_32 to Node_33:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:-0.00037499999999999974 stress:{'xx': -3.7499999999999973, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: -11.249999999999993
Truss: Node_33 to Node_34:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:-0.0005 stress:{'xx': -5.0, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: -15.0
Truss: Node_34 to Node_35:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:-0.0003750000000000001 stress:{'xx': -3.7500000000000013, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: -11.250000000000004
Truss: Node_27 to Node_32:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:-0.0007120003121097942 stress:{'xx': -7.120003121097942, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: -21.360009363293827
Truss: Node_28 to Node_33:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:-0.00035600015605489685 stress:{'xx': -3.5600015605489683, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: -10.680004681646905
Truss: Node_29 to Node_34:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:-1.7765477248433666e-19 stress:{'xx': -1.7765477248433666e-15, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: -5.3296431745301e-15
Truss: Node_30 to Node_35:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:0.00035600015605489685 stress:{'xx': 3.5600015605489683, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: 10.680004681646905
Truss: Node_28 to Node_32:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:0.0003560001560548972 stress:{'xx': 3.560001560548972, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: 10.680004681646915
Truss: Node_29 to Node_33:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:-2.0303402569638477e-19 stress:{'xx': -2.0303402569638477e-15, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: -6.091020770891543e-15
Truss: Node_30 to Node_34:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:-0.00035600015605489707 stress:{'xx': -3.5600015605489705, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: -10.680004681646912
Truss: Node_31 to Node_35:
material properties: FiberMaterial(Material)({'E': 10000.0, 'A': 3.0, 'nu': 0.0, 'fy': 1e+30}) strain:-0.0007120003121097942 stress:{'xx': -7.120003121097942, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
internal force: -21.360009363293827
Total running time of the script: (0 minutes 0.402 seconds)