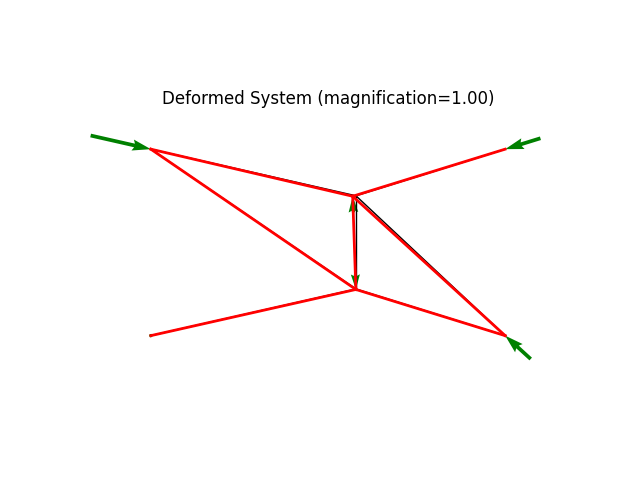
3d truss example demonstrating large deformation analysis.

The system is statically determined and allows for easy validation of calculated deformation, reactions and internal forces.

Author: Tatsu Sweet

Setup

from femedu.examples import Example

from femedu.domain import System, Node
from femedu.elements.finite import Truss
from femedu.materials import FiberMaterial
from femedu.solver import NewtonRaphsonSolver


class ExampleTruss04(Example):

    def problem(self):

        # initialize a system model
        params = {'E': 2100., 'A': 1., 'nu': 0.0, 'fy': 1.e30}

        model = System()

        # create nodes
        H = 5
        nd1 = Node(0.0, 5.0, 0.0)
        nd2 = Node(9.5, 5.0, 0.0)
        nd3 = Node(0.0, 0.0, 0.0)
        nd4 = Node(9.5, 0.0, 0.0)
        nd5 = Node(5.5, 3.75, H)
        nd6 = Node(5.5, 1.25, H)

        nodeList = [nd1, nd2, nd3, nd4, nd5, nd6]
        model.addNode(*nodeList)


        # create elements
        model.addElement(Truss(nd1, nd5, FiberMaterial(params)))  # bottom 1
        model.addElement(Truss(nd1, nd6, FiberMaterial(params)))  # up right diag 1
        model.addElement(Truss(nd2, nd5, FiberMaterial(params)))  # up left diag 1
        model.addElement(Truss(nd3, nd6, FiberMaterial(params)))  # bottom 1
        model.addElement(Truss(nd4, nd5, FiberMaterial(params)))  # up right diag 1
        model.addElement(Truss(nd4, nd6, FiberMaterial(params)))  # up left diag 1
        model.addElement(Truss(nd5, nd6, FiberMaterial(params)))  # bottom 1


        # define support(s)
        translation_dofs = ('ux', 'uy', 'uz')
        for node in [nd1, nd2, nd3, nd4]:
            node.fixDOF(*translation_dofs)

        # add loads
        nd5.setLoad((-100.0,), ('uz',))

        # analyze the model
        model.solve()

        # write out report
        model.report()

        # create plots
        model.plot(factor=1.)

Run the example by creating an instance of the problem and executing it by calling Example.run()

if __name__ == "__main__":
    ex = ExampleTruss04()
    ex.run()

System Analysis Report
=======================

Nodes:
---------------------
  Node_39:
      x:    [0. 5. 0.]
      fix:  ['ux', 'uy', 'uz']
      u:    [0. 0. 0.]
  Node_40:
      x:    [9.5 5.  0. ]
      fix:  ['ux', 'uy', 'uz']
      u:    [0. 0. 0.]
  Node_41:
      x:    [0. 0. 0.]
      fix:  ['ux', 'uy', 'uz']
      u:    [0. 0. 0.]
  Node_42:
      x:    [9.5 0.  0. ]
      fix:  ['ux', 'uy', 'uz']
      u:    [0. 0. 0.]
  Node_43:
      x:    [5.5  3.75 5.  ]
      P:    [   0.    0. -100.]
      u:    [-0.08746953 -0.01252906 -0.2503495 ]
  Node_44:
      x:    [5.5  1.25 5.  ]
      u:    [-0.00264455 -0.01179569  0.00083329]

Elements:
---------------------
  Truss: Node_39 to Node_43:
      material properties: FiberMaterial(Material)({'E': 2100.0, 'A': 1.0, 'nu': 0.0, 'fy': 1e+30})  strain:-0.030517537429943266   stress:{'xx': -64.08682860288086, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
      internal force: -64.08682860288086
  Truss: Node_39 to Node_44:
      material properties: FiberMaterial(Material)({'E': 2100.0, 'A': 1.0, 'nu': 0.0, 'fy': 1e+30})  strain:0.0004892637349850222   stress:{'xx': 1.0274538434685465, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
      internal force: 1.0274538434685465
  Truss: Node_40 to Node_43:
      material properties: FiberMaterial(Material)({'E': 2100.0, 'A': 1.0, 'nu': 0.0, 'fy': 1e+30})  strain:-0.02040406329686611   stress:{'xx': -42.84853292341884, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
      internal force: -42.84853292341884
  Truss: Node_41 to Node_44:
      material properties: FiberMaterial(Material)({'E': 2100.0, 'A': 1.0, 'nu': 0.0, 'fy': 1e+30})  strain:-0.00044111478214312256   stress:{'xx': -0.9263410425005574, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
      internal force: -0.9263410425005574
  Truss: Node_42 to Node_43:
      material properties: FiberMaterial(Material)({'E': 2100.0, 'A': 1.0, 'nu': 0.0, 'fy': 1e+30})  strain:-0.01687382151131819   stress:{'xx': -35.435025173768196, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
      internal force: -35.435025173768196
  Truss: Node_42 to Node_44:
      material properties: FiberMaterial(Material)({'E': 2100.0, 'A': 1.0, 'nu': 0.0, 'fy': 1e+30})  strain:1.7248299270645772e-06   stress:{'xx': 0.003622142846835612, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
      internal force: 0.003622142846835612
  Truss: Node_43 to Node_44:
      material properties: FiberMaterial(Material)({'E': 2100.0, 'A': 1.0, 'nu': 0.0, 'fy': 1e+30})  strain:0.005301537509333449   stress:{'xx': 11.133228769600242, 'yy': 0.0, 'zz': 0.0, 'xy': 0.0}
      internal force: 11.133228769600242