Note
Go to the end to download the full example code.
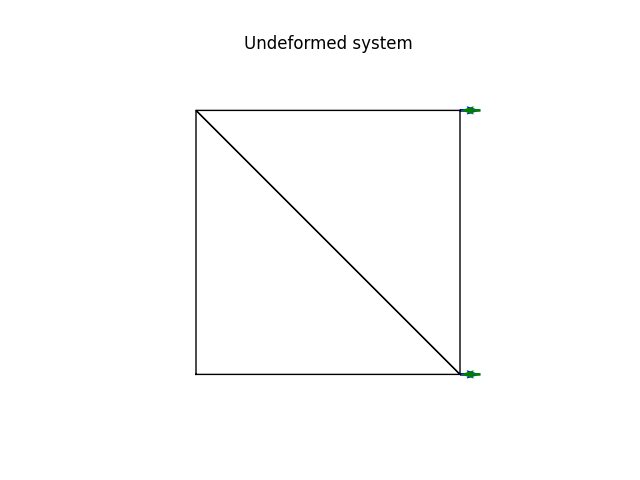
A square patch made of two triangular plate elements
- Basic implementation test with all prescribed displacements.
Testing the internal force computation.
v=-5 v=-5
| |
v v
3-----2 -> u=5
|\ b | >
| \ | >
| \ | > (w = 1.0)
| \ | >
| a \| >
0-----1 -> u=5
width: 10.
height: 10.
Material parameters: St. Venant-Kirchhoff, plane stress
E = 10.0
nu = 0.30
t = 1.0
Element loads:
node 0: [ 0.0, 0.0]
node 1: [ 5.0, 0.0]
node 2: [ 5.0, 0.0]
node 3: [ 0.0, 0.0]
Green Lagrange strain:
eps_XX = 0.5 * ((1.5)^2 - 1) = 0.625
eps_YY = 0.5 * ((0.5)^2 - 1) = -0.375
eps_XY = eps_YX = 0.000
eps_ZZ = - nu * (eps_XX + eps_YY) = -0.075
2nd Piola-Kirchhoff stress:
D = E t/(1 - nu^2) = 10.989
S_XX = (10.989) * ((0.625) + (0.30)(-0.375)) = 5.632
S_YY = (10.989) * ((-0.375) + (0.30)(0.625)) = -2.060
S_XY = S_YX = S_ZZ = 0.000
Author: Peter Mackenzie-Helnwein
from femedu.examples import Example
from femedu.domain import System, Node
from femedu.elements.linear import Triangle
from femedu.materials import PlaneStress
class ExamplePlate01(Example):
# sphinx_gallery_thumbnail_number = 2
def problem(self):
params = dict(
E = 10., # Young's modulus
nu = 0.3, # Poisson's ratio
t = 1.0, # thickness of the plate
fy = 1.e30 # yield stress
)
a = 10. # length of the plate in the x-direction
b = 10. # length of the plate in the y-direction
model = System()
nd0 = Node( 0.0, 0.0)
nd1 = Node( a, 0.0)
nd2 = Node( a, b)
nd3 = Node( 0.0, b)
model.addNode(nd0, nd1, nd2, nd3)
elemA = Triangle(nd0, nd1, nd3, PlaneStress(params))
elemB = Triangle(nd2, nd3, nd1, PlaneStress(params))
model.addElement(elemA, elemB)
elemB.setSurfaceLoad(face=2, pn=1.0)
model.plot(factor=0, title="Undeformed system", filename="plate01_undeformed.png", show_bc=1)
model.setLoadFactor(1.0)
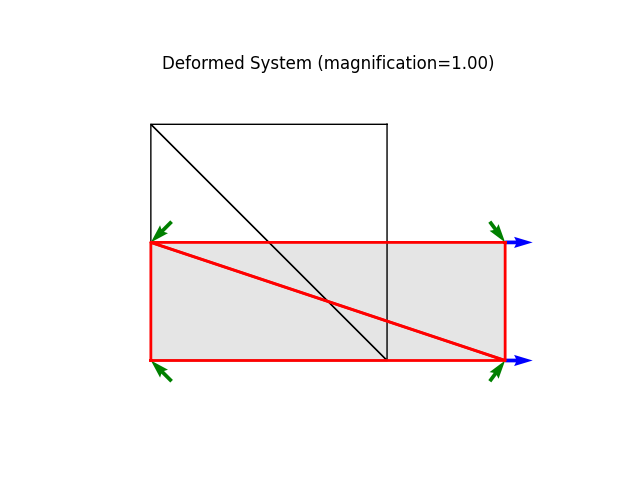
nd0.setDisp( [0.0, 0.0] )
nd1.setDisp( [5.0, 0.0] )
nd2.setDisp( [5.0,-5.0] )
nd3.setDisp( [0.0,-5.0] )
elemA.updateState()
elemB.updateState()
model.report()
model.plot(factor=1.0, filename="plate01_deformed.png")
Run the example by creating an instance of the problem and executing it by calling Example.run()
if __name__ == "__main__":
ex = ExamplePlate01()
ex.run()
System Analysis Report
=======================
Nodes:
---------------------
Node_593:
x: [0.000 0.000]
u: [0.000 0.000]
Node_594:
x: [10.000 0.000]
u: [5.000 0.000]
Node_595:
x: [10.000 10.000]
u: [5.000 -5.000]
Node_596:
x: [0.000 10.000]
u: [0.000 -5.000]
Elements:
---------------------
Triangle_832: nodes ( Node_593 Node_594 Node_596 )
material: PlaneStress
strain: xx=5.000e-01 yy=-5.000e-01 xy=0.000e+00 zz=-0.000e+00
stress: xx=3.846e+00 yy=-3.846e+00 xy=0.000e+00 zz=0.000e+00
Triangle_833: nodes ( Node_595 Node_596 Node_594 )
material: PlaneStress
strain: xx=5.000e-01 yy=-5.000e-01 xy=-0.000e+00 zz=-0.000e+00
stress: xx=3.846e+00 yy=-3.846e+00 xy=0.000e+00 zz=0.000e+00
Total running time of the script: (0 minutes 0.045 seconds)