Note
Go to the end to download the full example code.
Bending a cantilever beam using Quad elements
Using PatchMesher to model the beam
Background Theory
This problem can be approximately validated using Bernoulli-Euler theory for small deformations. The given problem shall be modeled using
parameter |
value |
description |
|---|---|---|
\(E\) |
modulus of elasticity (in ksi) |
|
\(I\) |
666.667 |
area moment of inertia (in \(inches^4\)) |
\(L\) |
length of the cantilever (in inches) |
|
\(P\) |
force at \(x=L\) (in kips) |
The general solution then yields
\[v(x) = -\frac{P L^3}{6 EI}\left( \frac{x}{L} \right)^2\left( 3 - \frac{x}{L} \right)\]
\[\theta(x) = \frac{d}{dx} v(x) = -\frac{P L^2}{2 EI}\left( \frac{x}{L} \right)\left( 2 - \frac{x}{L} \right)\]
\[M(x) = EI \frac{d}{dx} \theta(x) = -\frac{P L}{6} \left( 1 - \frac{x}{L} \right)\]
\[V(x) = \frac{d}{dx} M(x) = P\]
The horizontal movement follows as (\(2^{nd}\) order accurate)
\[u(x) = \int\limits_{0}^{x} -\frac{1}{2} \theta^2(s) \: ds
= -\frac{P^2 L^5}{120 (EI)^2}\left( \frac{x}{L} \right)^3\left( 20 - 15\:\frac{x}{L}+3 \left( \frac{x}{L} \right)^2 \right)\]
variable |
value |
description |
|---|---|---|
\(u(L)\) |
-0.0083981 |
end displacement (in inches). \(u>0\) means moving to the right. |
\(v(L)\) |
-1.296 |
end displacement (in inches). \(v>0\) means moving up. |
variable |
value |
description |
|---|---|---|
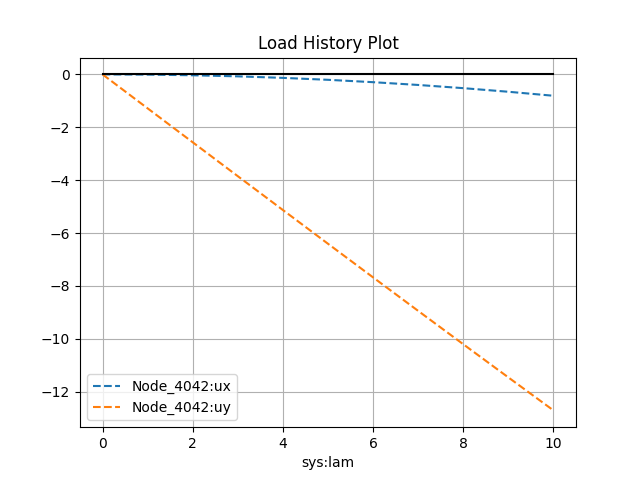
\(u(L)\) |
-0.83981 |
end displacement (in inches). \(u>0\) means moving to the right. |
\(v(L)\) |
-12.96 |
end displacement (in inches). \(v>0\) means moving up. |
import numpy as np
from femedu.examples import Example
from femedu.domain import System, Node
from femedu.solver import NewtonRaphsonSolver
#from femedu.elements.linear import Quad
from femedu.elements.finite import Quad
from femedu.materials import PlaneStress
from femedu.mesher import *
class ExamplePlate14(Example):
def problem(self):
# ========== setting mesh parameters ==============
Nx = 24 # number of elements in the mesh
Ny = 8 # number of elements in the mesh
Lx = 120.0 # length of plate in the x-direction
Ly = 20.0 # length of plate in the y-direction
# ========== setting material parameters ==============
params = dict(
E = 20000., # Young's modulus
nu = 0.250, # Poisson's ratio
t = 1.00 # thickness of the plate
)
# ========== setting load parameters ==============
px = 0.0 # uniform load normal to x=Lx
py = 0.0 # uniform load normal to y=Ly
pxy = 1.5 # uniform shear load on x=L
# ========== setting analysis parameters ==============
target_load_level = 10.00 # reference load
max_steps = 10 # number of load steps: 2 -> [0.0, 1.0]
# define a list of target load levels
load_levels = np.linspace(0, target_load_level, max_steps+1)
#
# ==== Build the system model ====
#
model = System()
model.setSolver(NewtonRaphsonSolver())
# create nodes
mesher = PatchMesher(model, (0.,0.),(Lx,0.),(Lx,Ly),(0.,Ly) )
nodes, elements = mesher.quadMesh(Nx, Ny, Quad, PlaneStress(params))
# define support(s)
## find nodes at x==0
for node, _ in model.findNodesAlongLine((0.0, 0.0), (0.0, 1.0)):
node.fixDOF('ux', 'uy')
# ==== complete the reference load ====
# the section at the right end
for _, face in model.findFacesAlongLine((Lx, 0.0), (0.0, 1.0), orientation=+1):
face.setLoad(px, -pxy)
# durface loading on the top face
for _, face in model.findFacesAlongLine((0.0, Ly), (1.0, 0.0), orientation=-1):
face.setLoad(-py, 0.0)
# find the node on the beam axis (y==Ly/2) at the end of the beam (x==Lx)
end_node, _ = model.findNodesAt((Lx, Ly/2))[0]
# set up a recorder
model.initRecorder(variables=['ux','uy'], nodes=[end_node])
model.startRecorder()
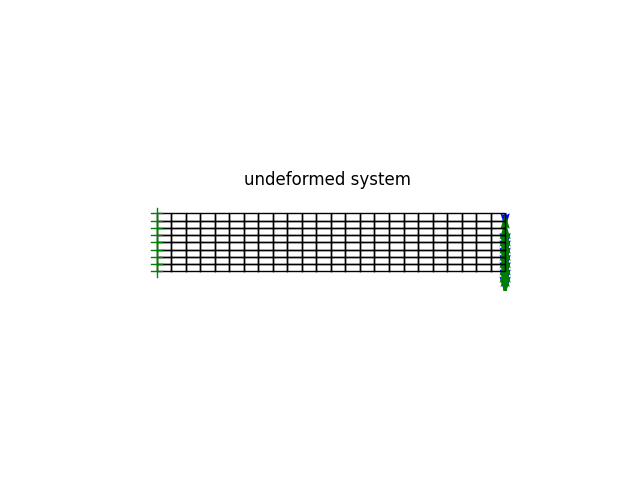
model.plot(factor=0, title="undeformed system", filename="plate11_undeformed.png", show_bc=1, show_loads=1)
for lf in load_levels:
model.setLoadFactor(lf)
model.solve(verbose=True)
#model.report()
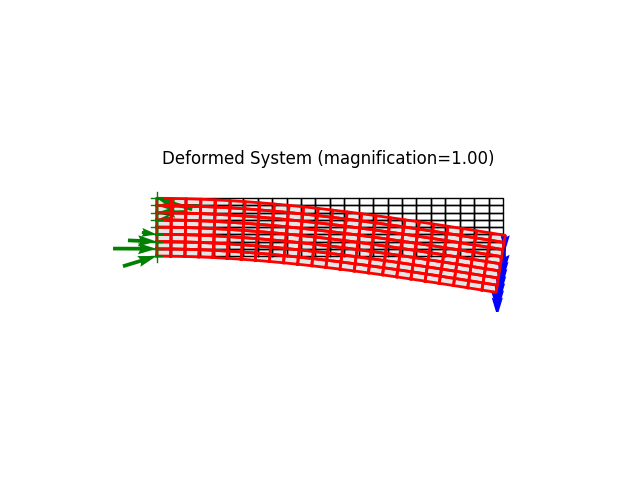
model.plot(factor=1., filename=f"plate11_deformed_lf{lf:.2f}.png", show_bc=1, show_loads=1, show_reactions=1)
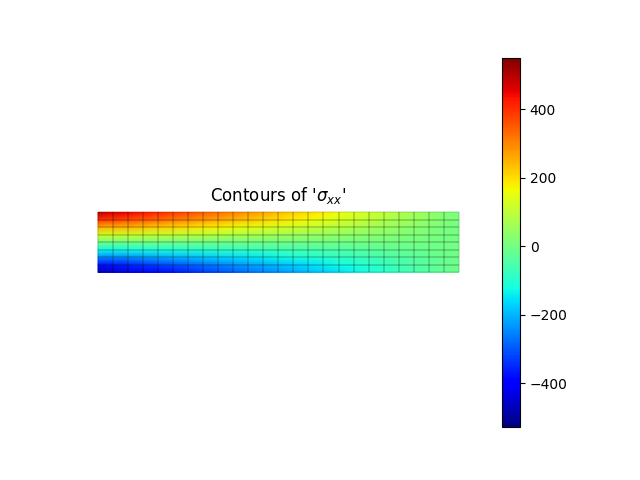
model.valuePlot('sxx', show_mesh=True)
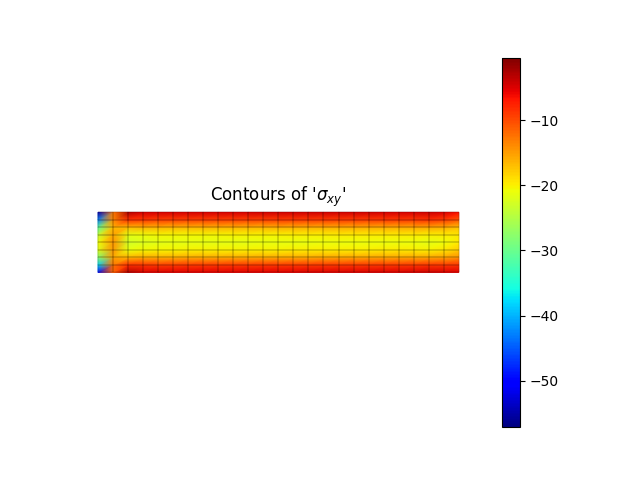
model.valuePlot('sxy', show_mesh=True)
# create a history plot for the end node
model.historyPlot('lam', ['ux','uy'], nodes=[end_node,end_node])
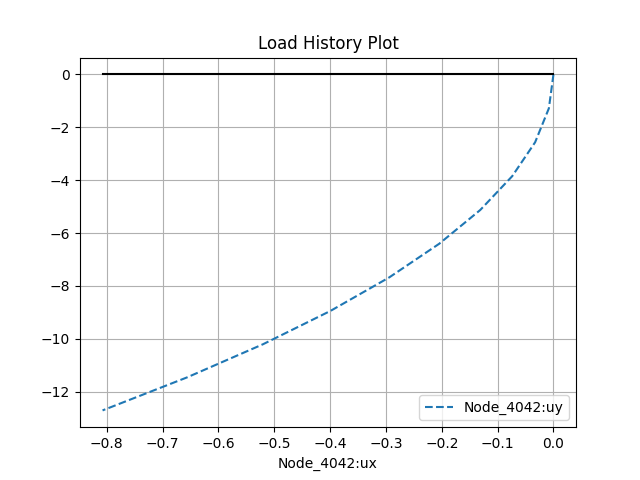
model.historyPlot(('ux',end_node), 'uy', node=end_node)
Run the example by creating an instance of the problem and executing it by calling Example.run()
if __name__ == "__main__":
ex = ExamplePlate14()
ex.run()
norm of the out-of-balance force: 1.2022e-09
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
norm of the out-of-balance force: 1.0270e+01
norm of the out-of-balance force: 7.7668e+01
norm of the out-of-balance force: 1.2854e-02
norm of the out-of-balance force: 2.4489e-09
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
norm of the out-of-balance force: 1.0270e+01
norm of the out-of-balance force: 7.7628e+01
norm of the out-of-balance force: 1.2849e-02
norm of the out-of-balance force: 1.1635e-08
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
norm of the out-of-balance force: 1.0270e+01
norm of the out-of-balance force: 7.7508e+01
norm of the out-of-balance force: 1.2833e-02
norm of the out-of-balance force: 4.1304e-08
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
norm of the out-of-balance force: 1.0270e+01
norm of the out-of-balance force: 7.7310e+01
norm of the out-of-balance force: 1.2805e-02
norm of the out-of-balance force: 8.9153e-08
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
norm of the out-of-balance force: 1.0270e+01
norm of the out-of-balance force: 7.7033e+01
norm of the out-of-balance force: 1.2766e-02
norm of the out-of-balance force: 1.5389e-07
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
norm of the out-of-balance force: 1.0270e+01
norm of the out-of-balance force: 7.6680e+01
norm of the out-of-balance force: 1.2715e-02
norm of the out-of-balance force: 2.3300e-07
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
norm of the out-of-balance force: 1.0270e+01
norm of the out-of-balance force: 7.6252e+01
norm of the out-of-balance force: 1.2653e-02
norm of the out-of-balance force: 3.2471e-07
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
norm of the out-of-balance force: 1.0270e+01
norm of the out-of-balance force: 7.5752e+01
norm of the out-of-balance force: 1.2579e-02
norm of the out-of-balance force: 4.2585e-07
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
norm of the out-of-balance force: 1.0270e+01
norm of the out-of-balance force: 7.5182e+01
norm of the out-of-balance force: 1.2493e-02
norm of the out-of-balance force: 5.3421e-07
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
norm of the out-of-balance force: 1.0270e+01
norm of the out-of-balance force: 7.4544e+01
norm of the out-of-balance force: 1.2394e-02
norm of the out-of-balance force: 6.4640e-07
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
Total running time of the script: (0 minutes 9.276 seconds)