Note
Go to the end to download the full example code.
Bending a cantilever beam using Quad9 elements
Using PatchMesher to model the beam
Background Theory
This problem can be approximately validated using Bernoulli-Euler theory for small deformations. The given problem shall be modeled using
parameter |
value |
description |
|---|---|---|
\(E\) |
modulus of elasticity (in ksi) |
|
\(I\) |
666.667 |
area moment of inertia (in \(inches^4\)) |
\(L\) |
length of the cantilever (in inches) |
|
\(P\) |
force at \(x=L\) (in kips) |
The general solution then yields
\[v(x) = -\frac{P L^3}{6 EI}\left( \frac{x}{L} \right)^2\left( 3 - \frac{x}{L} \right)\]
\[\theta(x) = \frac{d}{dx} v(x) = -\frac{P L^2}{2 EI}\left( \frac{x}{L} \right)\left( 2 - \frac{x}{L} \right)\]
\[M(x) = EI \frac{d}{dx} \theta(x) = -\frac{P L}{6} \left( 1 - \frac{x}{L} \right)\]
\[V(x) = \frac{d}{dx} M(x) = P\]
The horizontal movement follows as (\(2^{nd}\) order accurate)
\[u(x) = \int\limits_{0}^{x} -\frac{1}{2} \theta^2(s) \: ds
= -\frac{P^2 L^5}{120 (EI)^2}\left( \frac{x}{L} \right)^3\left( 20 - 15\:\frac{x}{L}+3 \left( \frac{x}{L} \right)^2 \right)\]
variable |
value |
description |
|---|---|---|
\(u(L)\) |
-0.0083981 |
end displacement (in inches). \(u>0\) means moving to the right. |
\(v(L)\) |
-1.296 |
end displacement (in inches). \(v>0\) means moving up. |
variable |
value |
description |
|---|---|---|
\(u(L)\) |
-0.83981 |
end displacement (in inches). \(u>0\) means moving to the right. |
\(v(L)\) |
-12.96 |
end displacement (in inches). \(v>0\) means moving up. |
import numpy as np
from femedu.examples import Example
from femedu.domain import System
from femedu.solver import NewtonRaphsonSolver
from femedu.elements.linear import Quad9
#from femedu.elements.finite import Quad9
from femedu.materials import PlaneStress
from femedu.mesher import *
class ExamplePlate15(Example):
def problem(self):
# ========== setting mesh parameters ==============
Nx = 4 # number of elements in the mesh
Ny = 4 # number of elements in the mesh
Lx = 120.0 # length of plate in the x-direction
Ly = 20.0 # length of plate in the y-direction
# ========== setting material parameters ==============
params = dict(
E=20000., # Young's modulus
nu=0.250, # Poisson's ratio
t=1.00 # thickness of the plate
)
# ========== setting load parameters ==============
px = 0.0 # uniform load normal to x=Lx
py = 0.0 # uniform load normal to y=Ly
pxy = 1.5 # uniform shear load on x=L
# ========== setting analysis parameters ==============
target_load_level = 10.00 # reference load
max_steps = 10 # number of load steps: 2 -> [0.0, 1.0]
# define a list of target load levels
load_levels = np.linspace(0, target_load_level, max_steps+1)
#
# ==== Build the system model ====
#
model = System()
model.setSolver(NewtonRaphsonSolver())
# create nodes
mesher = PatchMesher(model, (0., 0.), (Lx, 0.), (Lx, Ly), (0., Ly))
nodes, elements = mesher.quadMesh(Nx, Ny, Quad9, PlaneStress(params))
# define support(s)
## find nodes at x==0
for node, _ in model.findNodesAlongLine((0.0, 0.0), (0.0, 1.0)):
node.fixDOF('ux', 'uy')
# ==== complete the reference load ====
# the section at the right end
for _, face in model.findFacesAlongLine((Lx, 0.0), (0.0, 1.0), orientation=+1):
face.setLoad(px, -pxy)
# durface loading on the top face
for _, face in model.findFacesAlongLine((0.0, Ly), (1.0, 0.0), orientation=-1):
face.setLoad(-py, 0.0)
# find the node on the beam axis (y==Ly/2) at the end of the beam (x==Lx)
end_node, _ = model.findNodesAt((Lx, Ly / 2))[0]
# set up a recorder
model.initRecorder(variables=['ux', 'uy'], nodes=[end_node])
model.startRecorder()
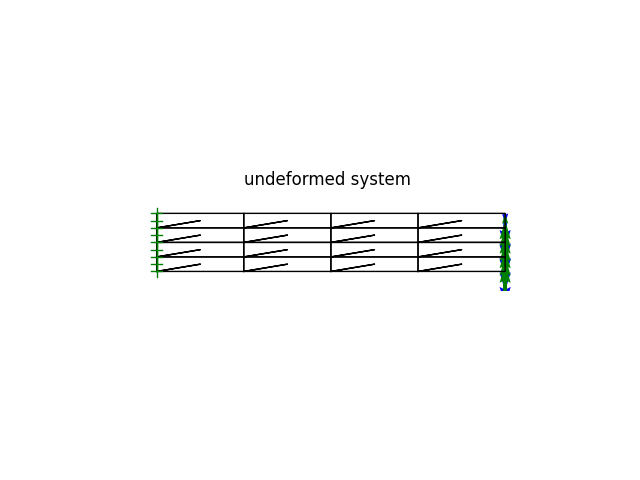
model.plot(factor=0, title="undeformed system", filename="plate11_undeformed.png", show_bc=1, show_loads=1)
for lf in load_levels:
model.setLoadFactor(lf)
for node, _ in model.findNodesAlongLine((Lx, 0.), (0., 1.)):
print(node)
for _, face in model.findFacesAlongLine((Lx, 0.), (0., 1.)):
print(face)
model.solve(verbose=True)
# model.report()
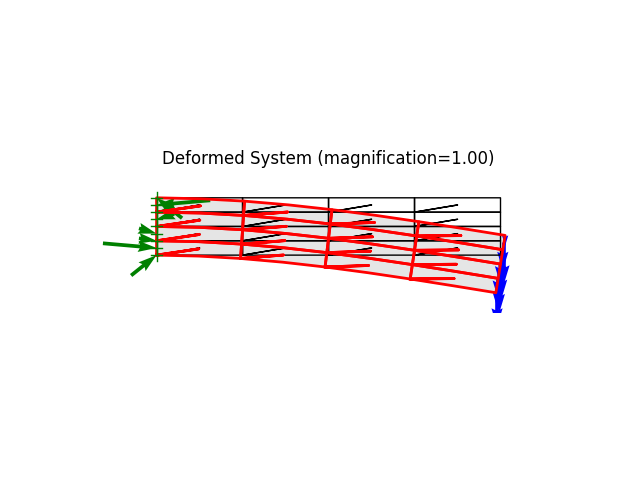
model.plot(factor=1., filename=f"plate11_deformed_lf{lf:.2f}.png", show_bc=1, show_loads=1, show_reactions=1)
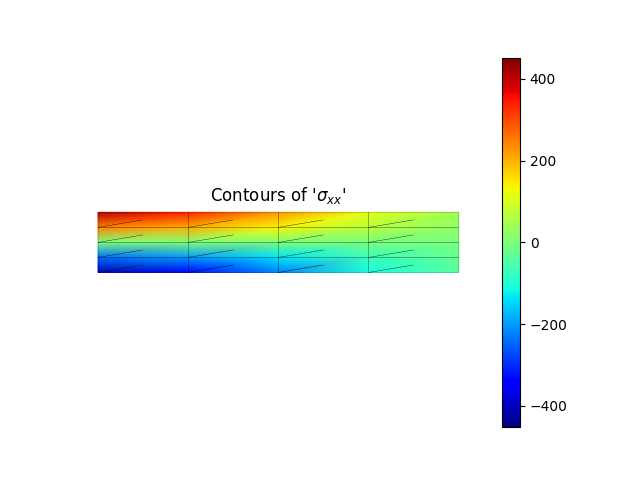
model.valuePlot('sxx', show_mesh=True)
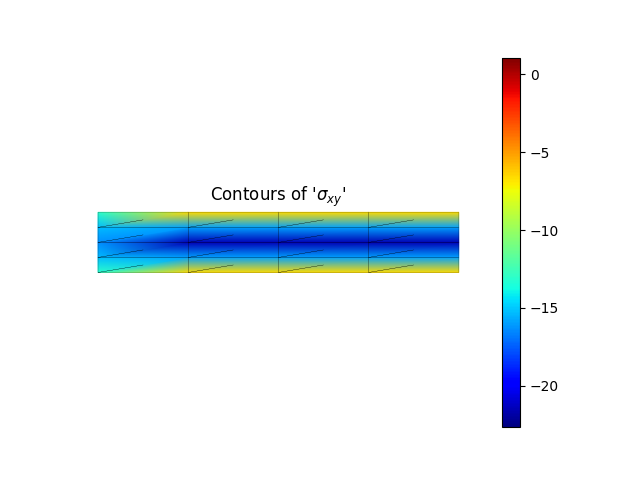
model.valuePlot('sxy', show_mesh=True)
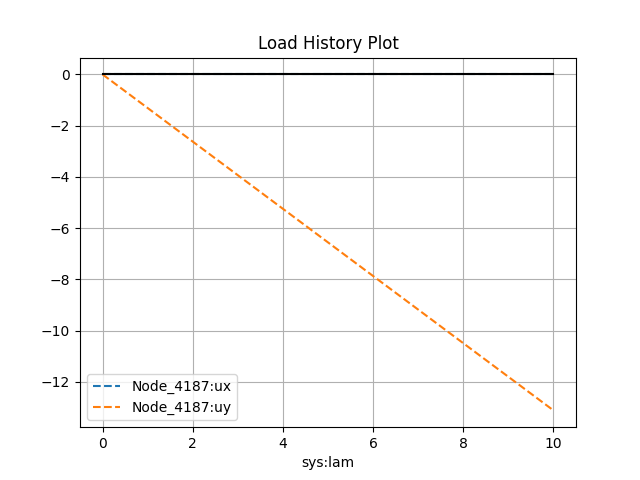
# create a history plot for the end node
model.historyPlot('lam', ['ux', 'uy'], nodes=[end_node, end_node])
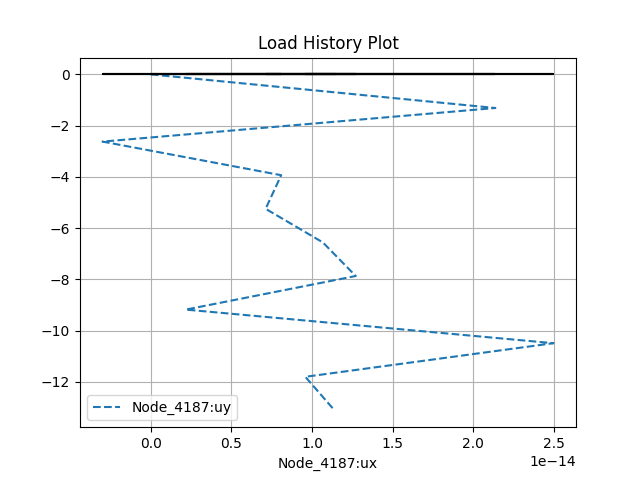
model.historyPlot(('ux', end_node), 'uy', node=end_node)
Run the example by creating an instance of the problem and executing it by calling Example.run()
if __name__ == "__main__":
ex = ExamplePlate15()
ex.run()
Node_4151:
x: [120.000 0.000]
u: [0.000 0.000]
Node_4160:
x: [120.000 2.500]
u: [0.000 0.000]
Node_4169:
x: [120.000 5.000]
u: [0.000 0.000]
Node_4178:
x: [120.000 7.500]
u: [0.000 0.000]
Node_4187:
x: [120.000 10.000]
u: [0.000 0.000]
Node_4196:
x: [120.000 12.500]
u: [0.000 0.000]
Node_4205:
x: [120.000 15.000]
u: [0.000 0.000]
Node_4214:
x: [120.000 17.500]
u: [0.000 0.000]
Node_4223:
x: [120.000 20.000]
u: [0.000 0.000]
Face2D_6738.1
Face2D_6742.1
Face2D_6746.1
Face2D_6750.1
norm of the out-of-balance force: 5.3029e-09
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
Node_4151:
x: [120.000 0.000]
u: [0.000 0.000]
Node_4160:
x: [120.000 2.500]
u: [0.000 0.000]
Node_4169:
x: [120.000 5.000]
u: [0.000 0.000]
Node_4178:
x: [120.000 7.500]
u: [0.000 0.000]
Node_4187:
x: [120.000 10.000]
u: [0.000 0.000]
Node_4196:
x: [120.000 12.500]
u: [0.000 0.000]
Node_4205:
x: [120.000 15.000]
u: [0.000 0.000]
Node_4214:
x: [120.000 17.500]
u: [0.000 0.000]
Node_4223:
x: [120.000 20.000]
u: [0.000 0.000]
Face2D_6738.1
Face2D_6742.1
Face2D_6746.1
Face2D_6750.1
norm of the out-of-balance force: 1.1040e+01
norm of the out-of-balance force: 5.2926e-09
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
Node_4151:
x: [120.000 0.000]
u: [-0.162 -1.312]
Node_4160:
x: [120.000 2.500]
u: [-0.121 -1.312]
Node_4169:
x: [120.000 5.000]
u: [-0.080 -1.312]
Node_4178:
x: [120.000 7.500]
u: [-0.040 -1.312]
Node_4187:
x: [120.000 10.000]
u: [0.000 -1.312]
Node_4196:
x: [120.000 12.500]
u: [0.040 -1.312]
Node_4205:
x: [120.000 15.000]
u: [0.080 -1.312]
Node_4214:
x: [120.000 17.500]
u: [0.121 -1.312]
Node_4223:
x: [120.000 20.000]
u: [0.162 -1.312]
Face2D_6738.1
Face2D_6742.1
Face2D_6746.1
Face2D_6750.1
norm of the out-of-balance force: 1.1040e+01
norm of the out-of-balance force: 6.0162e-09
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
Node_4151:
x: [120.000 0.000]
u: [-0.324 -2.624]
Node_4160:
x: [120.000 2.500]
u: [-0.242 -2.624]
Node_4169:
x: [120.000 5.000]
u: [-0.161 -2.624]
Node_4178:
x: [120.000 7.500]
u: [-0.080 -2.624]
Node_4187:
x: [120.000 10.000]
u: [0.000 -2.624]
Node_4196:
x: [120.000 12.500]
u: [0.080 -2.624]
Node_4205:
x: [120.000 15.000]
u: [0.161 -2.624]
Node_4214:
x: [120.000 17.500]
u: [0.242 -2.624]
Node_4223:
x: [120.000 20.000]
u: [0.324 -2.624]
Face2D_6738.1
Face2D_6742.1
Face2D_6746.1
Face2D_6750.1
norm of the out-of-balance force: 1.1040e+01
norm of the out-of-balance force: 6.8212e-09
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
Node_4151:
x: [120.000 0.000]
u: [-0.486 -3.936]
Node_4160:
x: [120.000 2.500]
u: [-0.363 -3.936]
Node_4169:
x: [120.000 5.000]
u: [-0.241 -3.936]
Node_4178:
x: [120.000 7.500]
u: [-0.121 -3.935]
Node_4187:
x: [120.000 10.000]
u: [0.000 -3.935]
Node_4196:
x: [120.000 12.500]
u: [0.121 -3.935]
Node_4205:
x: [120.000 15.000]
u: [0.241 -3.936]
Node_4214:
x: [120.000 17.500]
u: [0.363 -3.936]
Node_4223:
x: [120.000 20.000]
u: [0.486 -3.936]
Face2D_6738.1
Face2D_6742.1
Face2D_6746.1
Face2D_6750.1
norm of the out-of-balance force: 1.1040e+01
norm of the out-of-balance force: 5.8740e-09
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
Node_4151:
x: [120.000 0.000]
u: [-0.648 -5.248]
Node_4160:
x: [120.000 2.500]
u: [-0.484 -5.248]
Node_4169:
x: [120.000 5.000]
u: [-0.322 -5.247]
Node_4178:
x: [120.000 7.500]
u: [-0.161 -5.247]
Node_4187:
x: [120.000 10.000]
u: [0.000 -5.247]
Node_4196:
x: [120.000 12.500]
u: [0.161 -5.247]
Node_4205:
x: [120.000 15.000]
u: [0.322 -5.247]
Node_4214:
x: [120.000 17.500]
u: [0.484 -5.248]
Node_4223:
x: [120.000 20.000]
u: [0.648 -5.248]
Face2D_6738.1
Face2D_6742.1
Face2D_6746.1
Face2D_6750.1
norm of the out-of-balance force: 1.1040e+01
norm of the out-of-balance force: 5.0409e-09
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
Node_4151:
x: [120.000 0.000]
u: [-0.810 -6.560]
Node_4160:
x: [120.000 2.500]
u: [-0.605 -6.560]
Node_4169:
x: [120.000 5.000]
u: [-0.402 -6.559]
Node_4178:
x: [120.000 7.500]
u: [-0.201 -6.559]
Node_4187:
x: [120.000 10.000]
u: [0.000 -6.559]
Node_4196:
x: [120.000 12.500]
u: [0.201 -6.559]
Node_4205:
x: [120.000 15.000]
u: [0.402 -6.559]
Node_4214:
x: [120.000 17.500]
u: [0.605 -6.560]
Node_4223:
x: [120.000 20.000]
u: [0.810 -6.560]
Face2D_6738.1
Face2D_6742.1
Face2D_6746.1
Face2D_6750.1
norm of the out-of-balance force: 1.1040e+01
norm of the out-of-balance force: 4.7514e-09
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
Node_4151:
x: [120.000 0.000]
u: [-0.972 -7.872]
Node_4160:
x: [120.000 2.500]
u: [-0.726 -7.872]
Node_4169:
x: [120.000 5.000]
u: [-0.483 -7.871]
Node_4178:
x: [120.000 7.500]
u: [-0.241 -7.871]
Node_4187:
x: [120.000 10.000]
u: [0.000 -7.871]
Node_4196:
x: [120.000 12.500]
u: [0.241 -7.871]
Node_4205:
x: [120.000 15.000]
u: [0.483 -7.871]
Node_4214:
x: [120.000 17.500]
u: [0.726 -7.872]
Node_4223:
x: [120.000 20.000]
u: [0.972 -7.872]
Face2D_6738.1
Face2D_6742.1
Face2D_6746.1
Face2D_6750.1
norm of the out-of-balance force: 1.1040e+01
norm of the out-of-balance force: 6.5398e-09
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
Node_4151:
x: [120.000 0.000]
u: [-1.134 -9.184]
Node_4160:
x: [120.000 2.500]
u: [-0.847 -9.184]
Node_4169:
x: [120.000 5.000]
u: [-0.563 -9.183]
Node_4178:
x: [120.000 7.500]
u: [-0.281 -9.182]
Node_4187:
x: [120.000 10.000]
u: [0.000 -9.182]
Node_4196:
x: [120.000 12.500]
u: [0.281 -9.182]
Node_4205:
x: [120.000 15.000]
u: [0.563 -9.183]
Node_4214:
x: [120.000 17.500]
u: [0.847 -9.184]
Node_4223:
x: [120.000 20.000]
u: [1.134 -9.184]
Face2D_6738.1
Face2D_6742.1
Face2D_6746.1
Face2D_6750.1
norm of the out-of-balance force: 1.1040e+01
norm of the out-of-balance force: 4.9041e-09
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
Node_4151:
x: [120.000 0.000]
u: [-1.295 -10.497]
Node_4160:
x: [120.000 2.500]
u: [-0.968 -10.496]
Node_4169:
x: [120.000 5.000]
u: [-0.644 -10.495]
Node_4178:
x: [120.000 7.500]
u: [-0.321 -10.494]
Node_4187:
x: [120.000 10.000]
u: [0.000 -10.494]
Node_4196:
x: [120.000 12.500]
u: [0.321 -10.494]
Node_4205:
x: [120.000 15.000]
u: [0.644 -10.495]
Node_4214:
x: [120.000 17.500]
u: [0.968 -10.496]
Node_4223:
x: [120.000 20.000]
u: [1.295 -10.497]
Face2D_6738.1
Face2D_6742.1
Face2D_6746.1
Face2D_6750.1
norm of the out-of-balance force: 1.1040e+01
norm of the out-of-balance force: 4.9523e-09
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
Node_4151:
x: [120.000 0.000]
u: [-1.457 -11.809]
Node_4160:
x: [120.000 2.500]
u: [-1.089 -11.808]
Node_4169:
x: [120.000 5.000]
u: [-0.724 -11.807]
Node_4178:
x: [120.000 7.500]
u: [-0.362 -11.806]
Node_4187:
x: [120.000 10.000]
u: [0.000 -11.806]
Node_4196:
x: [120.000 12.500]
u: [0.362 -11.806]
Node_4205:
x: [120.000 15.000]
u: [0.724 -11.807]
Node_4214:
x: [120.000 17.500]
u: [1.089 -11.808]
Node_4223:
x: [120.000 20.000]
u: [1.457 -11.809]
Face2D_6738.1
Face2D_6742.1
Face2D_6746.1
Face2D_6750.1
norm of the out-of-balance force: 1.1040e+01
norm of the out-of-balance force: 4.5894e-09
Recorder.addData: 'stability' not initialized by the recorder: ignored
+
Total running time of the script: (0 minutes 1.511 seconds)