Benchmark problem: Wedged Plate - geometrically linear theory

Features

Using PatchMesher to model the plate
nodal boundary conditions using location-based search
face loads using location-based search
linear (small deformation) Triangle and Quad elements
history plot feature

import numpy as np

from femedu.examples import Example

from femedu.domain import System
from femedu.solver import NewtonRaphsonSolver, LinearSolver
from femedu.elements.linear import Quad, Triangle
from femedu.materials import PlaneStress
from femedu.mesher import *


class Example19_Benchmark01(Example):

    def problem(self):
        # ========== setting mesh parameters ==============

        Nx = 8  # number of elements in the mesh
        Ny = 4  # number of elements in the mesh
        L1 = 48.0
        L2 = 44.0
        L3 = 16.0

        # ========== setting material parameters ==============

        params = dict(
            E=1000.,  # Young's modulus
            nu=0.3,  # Poisson's ratio
            t=1.00  # thickness of the plate
        )

        # ========== setting load parameters ==============

        px = 0.0          # uniform load normal to x=Lx
        pxy = 100.0 / L3  # uniform shear load on x=L1

        # ========== setting analysis parameters ==============

        USE_NONLINEAR_SOLVER = False  # set to True if using an inelastic material

        target_load_level = 5.00  # reference load
        max_steps = 3  # number of load steps: 2 -> [0.0, 1.0]

        #
        # ==== Build the system model ====
        #

        model = System()
        if USE_NONLINEAR_SOLVER:
            model.setSolver(NewtonRaphsonSolver())
        else:
            model.setSolver(LinearSolver())

        # create nodes

        mesher = PatchMesher(model, (0., 0.), (L1, L2), (L1, L2 + L3), (0., L2))
        nodes, elements = mesher.quadMesh(Nx, Ny, Quad, PlaneStress(params))

        mesher.shift(1.25 * L1, 0.0)
        nodes2, elements2 = mesher.triangleMesh(Nx, Ny, Triangle, PlaneStress(params))

        nodes += nodes2
        elements += elements2

        # ==== Apply boundary conditions ====

        #
        # the left model
        #

        ## fix left side
        for node, _ in model.findNodesAlongLine((0.0, 0.0), (0.0, 1.0)):
            node.fixDOF('ux', 'uy')

        ## define loads ...
        for _, face in model.findFacesAlongLine((L1, 0.0), (0.0, 1.0), orientation=+1):
            face.setLoad(px, pxy)

        ## locate the node at the centerline
        nodeA, dist = model.findNodesAt((L1, L2 + L3))[0]

        #
        # the right model
        #

        ## fix left side
        for node, _ in model.findNodesAlongLine((1.25 * L1, 0.0), (0.0, 1.0)):
            node.fixDOF('ux', 'uy')

        ## define loads ...
        for _, face in model.findFacesAlongLine((2.25 * L1, 0.0), (0.0, 1.0), orientation=+1):
            face.setLoad(px, pxy)

        ## locate the node at the centerline
        nodeB, dist = model.findNodesAt((2.25 * L1, L2 + L3))[0]

        # model.report()

        # set up a recorder
        model.initRecorder(variables=['ux', 'uy'], nodes=[nodeA, nodeB])
        model.startRecorder()

        model.plot(factor=0, title="undeformed system", filename="benchmark01_undeformed.png", show_bc=1, show_loads=1)

        for lf in np.linspace(0.0, target_load_level, max_steps+1):
            model.setLoadFactor(lf)
            model.solve(verbose=True)

            # model.report()

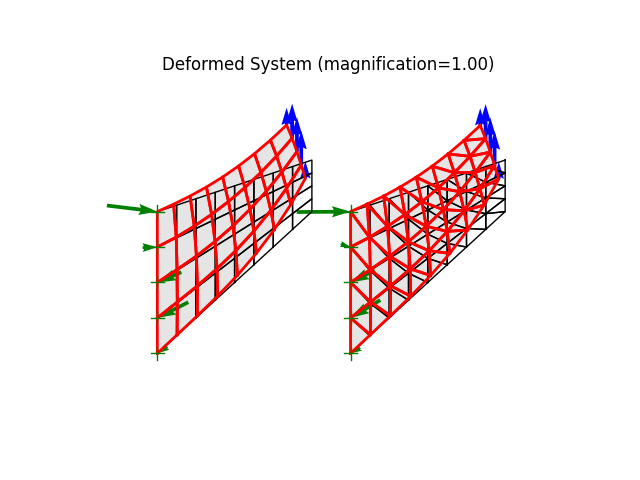
        model.plot(factor=1., filename=f"benchmark01_deformed_lf{lf:.2f}.png", show_bc=1, show_loads=1,
                   show_reactions=1)
        #
        # model.valuePlot('ux', filename=f"benchmark01_ux_lf{lf:.2f}.png")
        # model.valuePlot('uy', show_mesh=True, filename=f"benchmark01_uy_lf{lf:.2f}.png")
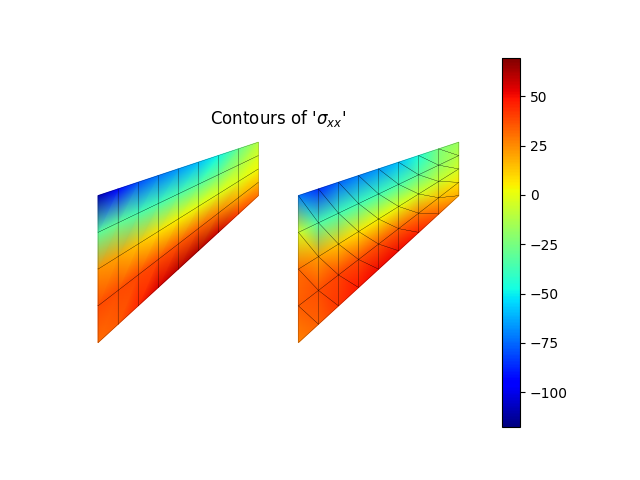
        model.valuePlot('sxx', show_mesh=True)
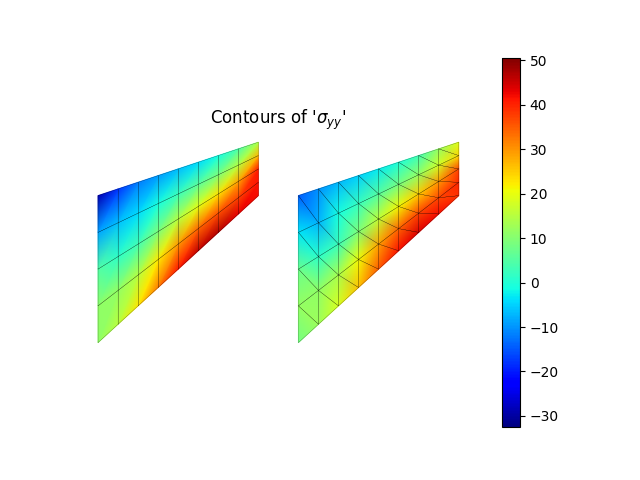
        model.valuePlot('syy', show_mesh=True)
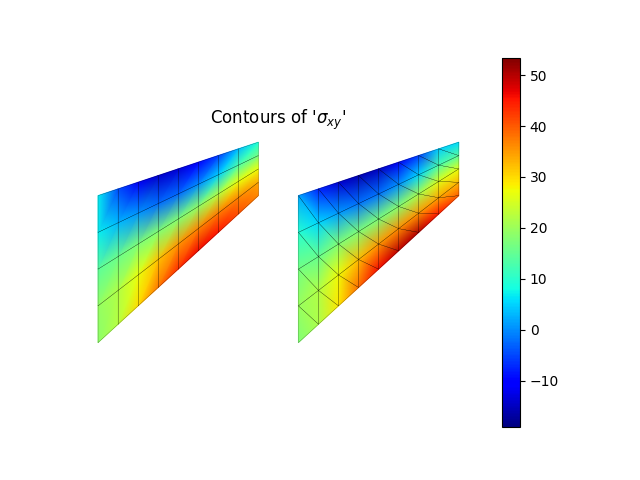
        model.valuePlot('sxy', show_mesh=True)

        # create a history plot for the end node

        # model.historyPlot('lam', ['ux','uy'], nodes=[nodeA,nodeA])
        # model.historyPlot('lam', ['ux','uy'], nodes=[nodeB,nodeB])
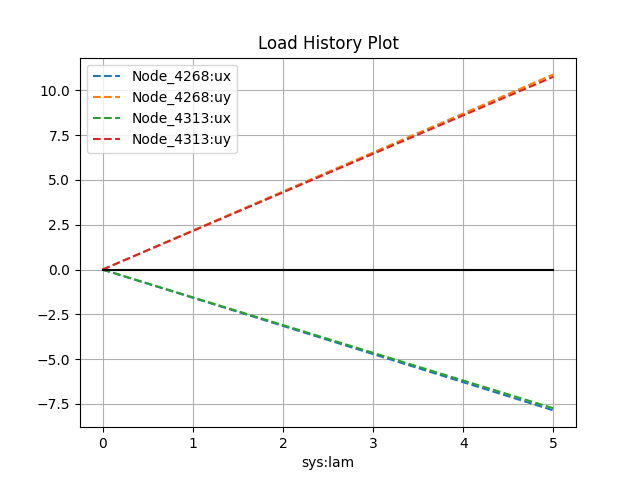
        model.historyPlot('lam', ['ux', 'uy', 'ux', 'uy'], nodes=[nodeA, nodeA, nodeB, nodeB])

Run the example by creating an instance of the problem and executing it by calling Example.run()

if __name__ == "__main__":
    ex = Example19_Benchmark01()
    ex.run()

$Contours of '$\sigma_{xx}$'$
$Contours of '$\sigma_{yy}$'$
$Contours of '$\sigma_{xy}$'$

+ Quad_6758: nodes ( Node_4231 Node_4232 Node_4241 Node_4240 )
    material: list
    strain (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Quad_6758: nodes ( Node_4231 Node_4232 Node_4241 Node_4240 )
    material: list
    strain (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Quad_6766: nodes ( Node_4240 Node_4241 Node_4250 Node_4249 )
    material: list
    strain (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Quad_6766: nodes ( Node_4240 Node_4241 Node_4250 Node_4249 )
    material: list
    strain (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Quad_6774: nodes ( Node_4249 Node_4250 Node_4259 Node_4258 )
    material: list
    strain (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Quad_6774: nodes ( Node_4249 Node_4250 Node_4259 Node_4258 )
    material: list
    strain (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Quad_6782: nodes ( Node_4258 Node_4259 Node_4268 Node_4267 )
    material: list
    strain (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Quad_6782: nodes ( Node_4258 Node_4259 Node_4268 Node_4267 )
    material: list
    strain (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (0): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (1): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (2): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
    strain (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress (3): xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_6797: nodes ( Node_4276 Node_4277 Node_4285 )
    material: PlaneStress
    strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_6798: nodes ( Node_4286 Node_4285 Node_4277 )
    material: PlaneStress
    strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_6798: nodes ( Node_4286 Node_4285 Node_4277 )
    material: PlaneStress
    strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_6813: nodes ( Node_4285 Node_4286 Node_4294 )
    material: PlaneStress
    strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_6814: nodes ( Node_4295 Node_4294 Node_4286 )
    material: PlaneStress
    strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_6814: nodes ( Node_4295 Node_4294 Node_4286 )
    material: PlaneStress
    strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_6829: nodes ( Node_4294 Node_4295 Node_4303 )
    material: PlaneStress
    strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_6830: nodes ( Node_4304 Node_4303 Node_4295 )
    material: PlaneStress
    strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_6830: nodes ( Node_4304 Node_4303 Node_4295 )
    material: PlaneStress
    strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_6845: nodes ( Node_4303 Node_4304 Node_4312 )
    material: PlaneStress
    strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_6846: nodes ( Node_4313 Node_4312 Node_4304 )
    material: PlaneStress
    strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
+ Triangle_6846: nodes ( Node_4313 Node_4312 Node_4304 )
    material: PlaneStress
    strain: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=-0.000e+00
    stress: xx=0.000e+00 yy=0.000e+00 xy=0.000e+00 zz=0.000e+00
Recorder.addData: 'stability' not initialized by the recorder: ignored
Recorder.addData: 'stability' not initialized by the recorder: ignored
Recorder.addData: 'stability' not initialized by the recorder: ignored
Recorder.addData: 'stability' not initialized by the recorder: ignored

Total running time of the script: (0 minutes 1.788 seconds)

Gallery generated by Sphinx-Gallery